初一数学期末复习综合练习二 班级 姓名
一、填空题
1、如果axa+1+4=-1是一元一次方程,则a=______
2、已知方程3x-2y=4,用含x的代数式表示y________
3、已知方程2 x-y+m-3=0的一个解是
,则m=________
4、方程3x+y=8的正整数解是____ （1）
5、已知代数式 ax3+bx+1,当x=2时,代数式的值为1, 当x= -2时,代数式的值为 ______
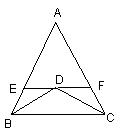
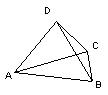
6、如图（1），△ABC中，AB=AC，BD、CD为角平分线，EF过D点，且EF∥BC，在这个图形中等腰三角形有
7、如果一个多边形除了一个内角外，其余各内角之和为2748°，
那么这个内角的度数是
8、已知3a一4b一11+(7a+6b+5)2=0，则a=______，b=_______。
（2）
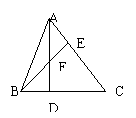
9、如图⑵，ΔABC中，∠CAB=52°，∠ABC=74°，AD⊥BC，
BE⊥AC，AD，BE交于F，则∠AFB=_____°
10、如图（3）已知等腰△ABC，AB=AC,BC＝1.5AB,△ABC的中线BD将△ABC 的周长分为两部分，它们之间的差为2cm，则△ABC的周长为____ （3）
11、在一个盛有白色小球的皮袋中,放了10个红球,小明从皮袋里取了3次,每次都有一个红球,共取了24个球,估计皮袋中共有_____个白色小球
12、下列图形⑴菱形⑵线段⑶平行四边形⑷角⑸正七边形中,共有___个是轴对称图形
13、在如图所示的2×2方格图案中有___正方形.,在3×3方格图案中有____正方形.
在4×4和5×5方格图案中有多少正方形.答: . .
在上面算法过程中你能否探索出用一般规律表示在n×n个方格
图案中的正方形个数表示为 .2
14、指出下列事件中,哪些是必然事件?哪些是不可能事事件?哪些是不确定事件?⑴明天的球赛巴西队一定赢__________⑵太阳从东方升起__________⑶一个长方体的体积是8,则它的长,宽,高分别是1,2,3______⑷在标准大气压下,温度在25°c时,水结冰______⑸一骑自行车的人骑至某十字路口,遇到”红灯”______
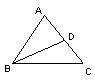
15、如图（4）在直角三角形中，∠C＝90°AB的垂直平分线交AC于D，如果∠CBD＝24°，△ABC的周长为30cm,AB＝12cm，
则∠A=_____,△BCD的周长为_______
16、如图，AB=AC=AD，如果∠DAC是∠CAB的k倍，那么∠DBC是∠BDC的 倍
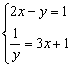二、选择题
1、在方程组⑴
⑵
⑶ 
⑷
中,属于二元一次方程组的是
()
A ⑶ B ⑴⑶ C ⑵⑶ D ⑵⑶⑷
2、已知三条线段a>b>c>0,它们能组成三角形的条件是 ( )
A a=b+c B a+c>b C b-c>a D a-b<c
3、为了了解一批产品的质量，从中抽取300个产品进行检验，在这个问题中，300个产品的质量叫做 （ ）
A 总体 B 个体 C 总体的一个样本 D 普查方式
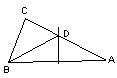
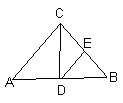4、如图，△ABC是等腰直角三角形，∠C=90°，CD是底边上的高，DE⊥CB，则图中等腰直角三角形共有
（ ）
A 3 个 B 4 个 C 5 个 D 6 个
5、锐角三角形中,任意两个锐角的和必大于 ( )
A 90° B 100° C 110 ° D 120°
6、关于x,y的二元一次方程组
没有解时,则a取值为
( )
A a=0 B a=-6 C a=6 D a=1
三、解方程
（1）
（2）
（3）
（4）2-x+1=3
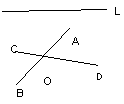
四、已知，直线L和相交于O点的直线AB,CD，
求作：L上一点P，使P到AB,CD的距离相等
五、已知，如图，△ABC中，∠ACB=90°,CA=CB,点D在AB上，点E在BC上，且DC=DE,∠2=2∠1,求∠1的度数
六、解答题
（1）已知
是关于x、y的一元一次方程，且m、n满足
，求a、b的值
（2）下表是某周甲、乙两种股票的收盘价（每天结束交易时的价格，单位：元/股）
| 时间 种类 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 甲 | 14．9 | 14．75 | 14．45 | 14．05 | 14．85 |
| 乙 | 15．4 | 15．15 | 15．9 | 15．6 | 15．5 |
在该周内，小张持有的甲、乙两种股票若干（每种股票数量保持不变），按这两种股票的收盘价计算，小张两种股票的总价星期四比星期三亏了1000元，星期五比星期四盈600元，问：小张该周内持有甲、乙两种股票各多少股？
（3）如果一个图形绕着一个定点旋转一个角α（0°﹤α﹤180°）能够与原来的图形重合，那么这个图形就叫做旋转对称图形。例如，正三角形绕着它的中心旋转120°（如图1）能够与原来的正三角形重合，因而正三角形是旋转对称图形。图2是一个五叶风车的示意图，它也是旋转对称图形（α=72°）。
显然，中心对称图形都是旋转对称图形，但旋转对称图形不一定是中心对称图形。下面四个图形中，是旋转对称图形的有 （填序号）
（4）如表，方程1，方程2，方程3，…是按照一定规律排列的一列方程：
①若方程
的解是
，求a、b的值，该方程是不是表中所给出的一列方程中的一个方程？如果是，它是第几个方程？
②请写出这列方程中的第n个方程和它的解，并验证所写出的解适合第n个方程
| 序号 | 方程 | 方程的解 | |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| ﹕ | ﹕ | ﹕ | ﹕ |
（5）、有四张相同的纸片，其中三张上各画一个相同的正三角形，另一张纸片画一个正方形。将这四张纸片放在一个盒子里搅匀，随机地抽取两张纸片，可能拼成一个菱形（取出的是两张画三角形的纸片），也可能拼成一个房子（取出的是一张画三角形一张画正方形的纸片）。这个游戏规则是这样的：若拼成一个菱形，甲赢；若拼成一个房子，乙赢。你认为这个游戏是公平的吗？说明理由。
（6）、在“三峡明珠”宜昌市蕴含有丰富的水电、旅游资源。三峡工程等多座大型水电站建于此，随着2003年首批机组发电，估计当年将有200万人次来参观三峡大坝（参观门票按每张50元计），由此获得的旅游总收入可达7．025亿元，相当于当年三峡工程发电收入的26%，（每度电收入按0．1元计）据测算，每度电可创产值5元，而每10万元就可以提供一个就业岗位，待三峡工程全部建成后，其年发电量比2003年宜昌市所有发电站的年发电总量还多75%，并且是2003年宜昌是（除三峡工程外）其他发电站年发电两的4倍。
（1） 2003年三峡工程的年发电量是 _____________ 亿度。
（2） 设2003年其他发电站共发电x度，由题意列方程得
求得x= 亿元；从而三峡工程全部建成后该工程的年发电量是 亿元
（3） 旅游部门测算总收入是以门票收入为基础，再按一定比值确定其他收入（吃、住、行、购物、娱乐的收入），两者之和即为旅游总收入；由题意得2003年的其他收入与门票收入的比值是 。
（4） 请你估计三峡工程全部建成后，由三峡工程年发电量提供的就业岗位有多少个？