七年级数学下学期期末试卷
班级 学号 姓名 得分
一、填空题（每空2分，共30分）
1．在代数式
中，单项式有 个；次数为2的单项式是
；系数为1的单项式是
。
2．计算：
=
。
3．计算：8100×0.125100 = 。
4．某种细胞的直径为0.000,000,000,001,05米，这个数用科学记数法表示为
米。
5．北京市土地面积为16807.8千米2。这个数保留2个有效数字的近似数是
千米2。
6．如图，∠1=65°，∠3+∠4=180°，则∠2= °。
 |
7．如图，ΔABD≌ΔACE，点B和点C是对应顶点，AB=8
，BD=7,AD=3，则AC=_____。
8．在ΔABC中，AB=3，BC=7，则AC边的取值范围是
。
9．如图，∠A＝29°，∠B＝44°，则∠1＝
10．假如小猫在如图所示的地板上自由地走来走去，并随意停留在某块方砖上，它最终停留在黑色方砖上的概率是 （图中每一块方砖除颜色外完全相同）。
11．据世界人口组织公布，地球上的人口从1600年到1999年一直呈递增趋势，即随时间的增加，地球上的人口数量在逐渐地增加，如果用t表示时间，y表示人口数量，那么 是自变量， 是因变量。
12．如图，ΔABC中，AB的垂直平分线交AC与点M。若CM=3，BC=4，AM=5，则ΔMBC的周长=_____________。．
二、选择题（每小题8分，共24分）
13．地球绕太阳每小时转动通过的路程约是
，用科学记数法表示地球一天（以24小时计）转动通过的路程约是（ ）
A．
B．
C．
D．
14．计算
的结果是（ ）
A．
B．
C．
D．
15．掷一颗均匀的骰子，6点朝上的概率为（ ）
A．0
B．
C．1
D．
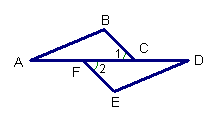
16．如图，已知：
，
，下列条件中能使ΔABC≌ΔDEF的是（ ）
A．
B．
C．
D．
17．下列图形中对称轴最多的是（ ）
A．线段 B．等边三角形
C．正方形 D．钝角
18．墙上有一面镜子，镜子对面的墙上有一个数字式电子钟。如果在镜子里看到该电子钟的时间显示如图所示，那么它的实际时间是（ ）
A．12∶51 B．15∶21 C．15∶51 D．12∶21
 |
19．小强和小敏练短跑，小敏在小强前面12米。如图，OA、BA分别表示小强、
小敏在短跑中的距离S（单位：米）与时间t（单位：秒）的变量关系的图象。
根据图象判断小强的速度比小敏的速度每秒快（ ）
A．2.5米 B．2米 C．1.5米 D．1米
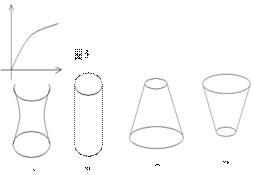
20、向高为h的水瓶中注水，注满为止，如果注水量y与水深x的关系如图5，则水瓶形状应为图中的（
）
三、计算（每题4分，共20分）
21．
；
22．
；
23．
÷
； 25．
；
26．已知一个角的余角比它的补角的
小18°，求这个角。
四、操作题（每题4分，共8分）
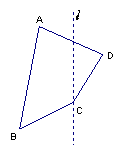
27．请你以虚线
为对称轴画出四边形
ABCD的对称图形：
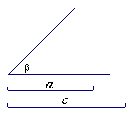28．已知：线段
、
和∠β（如图），利用直尺和圆规作ΔABC，使BC=，AB=，∠ABC=∠β。（不写作法，保留作图痕迹）。
五、（本题6分）
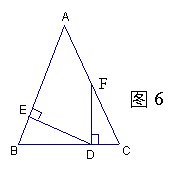
如图6，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，∠AFD=158°，则∠EDF为多少度？.
六、（本题6分）
30．图为一位旅行者在早晨８时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
（1）在这个变化过程中，自变量是____，因变量是______。
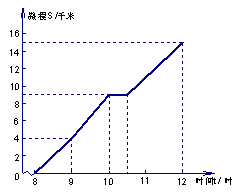（2）９时，１０时３０分，１２时所走的路程分别是多少？
（3）他休息了多长时间？
（4）他从休息后直至到达目的地这段时间的平均速度是多少？
七、（本题6分）
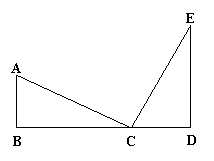
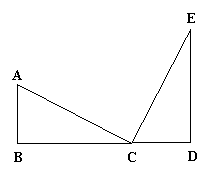31．如图，已知：
，
，
，
，那么AC与CE有什么关系？写出你的猜想并说明理由。