七年级数学（下）期末考试试卷
班级 姓名 得分_______
一、精心选一选（每小题3分，共18分）
1.某市科学知识竞赛的预赛中共20道选择题,答对一题得10分,满分200分, 答错或不答扣5分,总得分不少于80分者就通过预赛而进入决赛,若小王通过了预赛,那么他至少答对了( )
A.10道题 B.12道题 C.14道题 D.16道题
2．已知关于x的方程2x=8与x+2＝-k的解相同，则代数式
的值是 ( )
A.-
B.
C.- D.
3．若(3x-y+1)2与｜2x+3y-25｜互为相反数，那么(x-y)2的值为( )
A.81 B. 25 C. 5 D.49
4．四边形ABCD中，若∠A+∠C＝180°且∠B:∠C:∠D＝3:5:6，则∠A为（ ）.
A.80° B.70° C. 60° D.50°
5．某人到瓷砖店购买一种正多边形的瓷砖,铺设无缝地板,他购买的瓷砖形状不可以是（ ）
A.正三角形 B.正四边形 C.正六边形 D.正八边形
6．掷二枚骰子，得到的点数和为4的成功率（机会）记为a，得的点数和为5的的成功率（机会）记为b，则a与b的大小关系是( )
A．a=b B。a<b C。a>b D。不能确定
二、耐心填一填:（每小题2分，共24分）
7．如果单项式
ax+1b4与9 a2x-1b4是同类项，则x= .
8．由3x-2y=5可得到用x表示y的式子是 .
9.不等式5x-2<3(x+6)的最大整数解是__________.
10．若
是方程x-ky＝0的解，则k＝ .
11．一个三角形最多有a个锐角，b个直角，c个钝角，则a+b+c= .
12．在刚做好的门框架上，工人师傅为了避免门框变形，在矩形的框架上斜钉一根木条，这是利用 原理.
13．已知△ABC中，∠A＝
∠B＝
∠C，则△ABC是 三角形.
14.关于x的方程kx+15=6x+13的解为负数,则k的取值范围是_________.
15．某商品按原价的八折出售，售价为14.80元，那么原定价为 _______元.
16．一个多边形的每一个外角都等于36°，那么这个多边形的内角和是 °.
17．等腰三角形两边长分别是5cm 和8cm，则其周长是 .
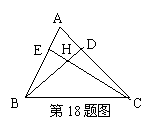
18．已知：如图，在△ABC中，∠A＝55°,H是高BD、CE的交点，则∠BHC＝ .
三、看准了再做！(每小题5分,共15分)
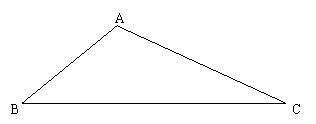
19．已知△ABC，请你作出△ABC的高CD，中线BF，角平分线AE（不写画法）.
 |
20. 观察以下图形，回答问题：
（1）图②有 个三角形；图③有___ _ 个三角形；图④有___ _个三角形；……
猜测第七个图形中共有 个三角形.
（2）按上面的方法继续下去，第
个图形中有 个三角形（用的代数式表示结论）.
21．世界杯决赛分成8组，每小组4个队，小组进行单循环（每个队都与该小组的其他队比赛一场）比赛，选出2个对进入16强。胜一场得3分，平一场得1分，负一场得0分。请问：
（1）每小组共比赛 场
（2）在小组比赛中，现有一队得到6分，该队出线是一个 事件。
四、细心算一算 (每小题5分,共20分)
22．解方程：
23. 解方程组：
24.求不等式
的正整数解. 25.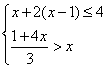
(解集在数轴上表示出来)
五、探索发现(每小题7分，共14分)
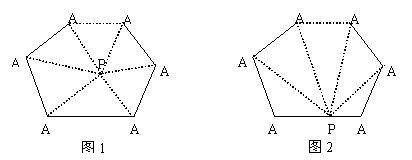
26．小明和小方分别设计了一种求n边形的内角和（n-2）×180°（n为大于2的整数）的方案：
（1） 小明是在n边形内取一点P，然后分别连结PA1、PA2、…、PAn（如图1）；
（2） 小红是在n边形的一边A1A2上任取一点P，分别连结PA4、PA5、…、PA1（如图2）.
请你评判这两种方案是否可行？如果不行的话，请你说明理由；如果可行的话，请你沿着方案的设计思路把多边形的内角和求出来.
 |
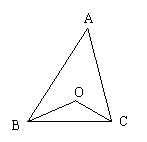27、如图，在△ABC中，∠ABC、∠ACB的平分线交于O点.
① 当∠A=300时，∠BOC=105°=
；
② 当∠A=400时， ∠BOC=110°=
③ 当∠A=500时， ∠BOC=115°=
当∠A=n0 (n为已知数)时，猜测∠BOC= ，并用所学的三角形的有关知识说明理由.
六、让数学为我们服务
28、(本小题9分)将一筐橘子分给若干个小朋友，如果每人4个，则剩余9个：如果每人分6个，则最后一位小朋友分的的个数将小于3个。求小朋友的人数与桔子的总数。
29．（本小题10分）现有甲、乙两家商店出售茶瓶和茶杯，茶瓶每只价格为20元，茶杯每只5元。已知甲店制定的优惠方法是买一只茶瓶送一只茶杯；乙店按总价的92%付款。某单位办公室需购茶瓶4只，茶杯若干只（不少于4只）。
(1)当需购买40只茶杯时，若让你去办这件事，你将打算去哪家商店购买，为什么？
(2)当购买茶杯多少只时，两种优惠方法的效果是一样的？
30．（本题满分10分）某蔬菜公司收购到某种蔬菜140吨，准备加工后上市销售。已知每吨蔬菜粗加工后的利润为1000元，精加工后的利润为2000元，该公司的加工能力是：每天可以精加工6吨或者粗加工16吨。现有15天时间可以用来加工这种蔬菜。如何合理安排粗加工和精加工的时间，才能使公司恰好在15天内将蔬菜全部加工完？该公司出售这些加工后的蔬菜共可获利多少元？