初一数学文化素质测试试卷
出卷人：王韶荣 审题人：陆伟林
一、填空题（每空2分，共40分）
1、一天早晨的气温是 -18ºC，上午上升了4ºC，晚上又下降了6ºC，则晚上的气温是__________ºC。
2、绝对值等于3的整数是__________。平方等于16的数是 。立方等于本身的数有 。
3、我国18岁以下的未成年人约有人。此数据用科学记数法可表示为 。
4、近似数11亿精确到 位，有 个有效数字。
5、一个两位数，若它的十位数字是
，个位数字是
，用含有
的代数式表示这个两位数是 。
6、x－2＋（y＋3）2＝0，则yx＝ 。
7、在墙上固定一根木条，至少要钉 个铁钉，理由是 。
8、三条直线两两相交有 个交点。
9、已知线段AB=7厘米，在直线AB上截取AC=1.5厘米，则BC= 。
10、如图，点A、B、C、D在同一直线上，则图中有 条直线，有 条线段，有 条射线。
11、已知数轴上的A点到原点的距离是3，那么在数轴上到A点的距离是2的点表示的数是_________。
12、某商品的进价是400元，标价是600元，实际是以7折销售的，在这次交易中，商家的盈利是 元。
13、某种细菌在培养过程中，每1小时分裂1次（由1个分裂成2个）。若这种细菌由1个分裂成32个，那么这个过程需经过 小时。
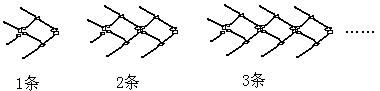
14、如图是小红用火柴搭的1条、2条、3条……“金鱼”，按此规律搭n条“金鱼”需要火柴 根。
二、选择题（每题3分，共18分）
1、下列说法错误的是……………………………………（ ）
A、0既不是正数也不是负数 B、正整数和负整数统称整数
C、整数和分数统称有理数 D、正有理数包括正整数和正分数
2、一种面粉的质量标识为“25±0.25千克”，则下列面粉中合格的有……………………………………………………………（ ）
A、24.70千克 B、25.30千克 C、25.51千克 D、24.80千克
3、下列各组代数式中，是同类项的一组是………………（ ）
A、
与
B、与
C、与
D、与
4、下列说法正确的是…………………………………………（ ）
A、射线是向两方无限延伸的 B、可以用直线上的一个点来表示该直线
C、射线AB也可以写成射线BA D、线段AB和线段BA是指同一条线段
5、在直线上顺次取A、B、C三点，使得AB=9cm，BC=4cm，如果O是线段AC的中点，则线段OB的长是…………………………………………………………………………（ ）
A、2.5cm B、1.5cm C、3.5cm D、5cm
6、下列各图经过折叠后不能围成一个无盖正方体的是 …………（ ）
 |  | ||||||
 | |||||||
 | |||||||
A B C D
三、计算题（每题3分，共12分）
（1） （-4）+（+5）+（-10）+（+4）
（2） 2÷（
）×
÷（－5
）
（3） （
―3―
＋
）÷（－
） （4） （―1）5―（―3）2―（―32）
四、合并同类项（每题3分，共12分）
（1）x－（3x＋y）＋（x－5y） （2）3a―[8a―（5a―2c）]＋2c
（3）6a2b＋2ab－3a2b2＋9a－3ba－4a2b2－6a2b
（4）先化简再求值：
3x2y―[2x2y―（2xyz―x2y）―4x2z]―xyz，其中x=-2，y=-3，z=1。
五、作图题（4分）
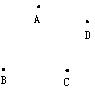
如图，已知点A、B、C、D，读下列语句并画图。
1、 画线段AB；
2、 连结AC、BD，交于点O；
3、 以B为端点，画射线BC；
4、作直线AD，交射线BC于点E。
六、探索与推断（3分）
观察下列各式的运算结果，归纳出来尾数字是5的正整数，它们的平方运算有何规律。请将总结出来的规律用自然数n表示成一个运算公式。
52=25 152=125 252=625 352=1225 452=2025 552=3025
七、已知，如图线段AB=8cm，C是AB上的一点，且AC=3.2cm，又知M是AB的中点，N是AC的中点，求MN的长。（5分）
八、“十一”黄金周期间，某校4名教师和10名学生组成旅游团，外出旅游，甲旅行社收费标准是：一律八折优惠，乙旅行社收费标准是：若4人买全票，其余人按七折优惠，这两家旅行社的全票价格均为每人300元；你认为应该去哪家旅行社较合算？（6分）
附加题：（共20分）
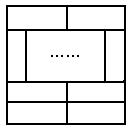
1、右图是若干个完全相同的小长方形拼成的一个正方形，那么图中共有 个小长方形。（3分）
2、在一张挂历上，任意圈出一个竖列上相邻3个数的和不可能是（ ）（3分）
A．60 B．39 C．40 D．57
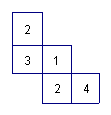3、如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图。（3分）
4、观察按x的升幂排列的多项式1-3x2+5x4-7x6+……，并回答下列问题：
（1）它的第1997和第2000项各是什么？（2分）
（2）它的第R和第R+1项各是什么？（R为正整数）（2分）
（3）当x=-1时，求它的前2003项的和。（2分）
5、数学课上王老师讲了我国古代数学家刘徽在公元3世纪用“割圆术”求得π的近似值是3.14后，出了一道计算题：“求+
+
+
+……的值”。李明经认真思考后很快得出了结果，请你写出他的解题过程。（5分）