初一数学期末复习（七）
一、填空题（每小题2分，共20分）
1．如图，已知CB＝4，DB＝7，D是AC的中点，
则AC＝_________ .
2．实施西部大开发战略是党中央面向21世纪的重大决策，我国西部地区面积为平方千米，用科学计数法表示这个面积 平方千米。
3．已知数轴上表示-2与-8的两点分别是A、B那么A、B两点间的距离是 。
4．甲、乙两个正方体的棱长分别为4.75cm和3.38cm，那么它们的体积之差为 cm3(保留3个有效数字。
5．用x表示人的年龄，代数式
)表示人在运动时所能承受的每分钟心跳的最高次数。若一个15岁的学生运动时每分钟的心跳为150次，那么他
危险（填“有”或“没有”）。
 |
6．如图所示，用同样规格的黑、白两色正方形瓷砖铺设矩形地面，请观察下图：则第n个图形中需用黑色瓷砖块 .（用含n的代数式表示）
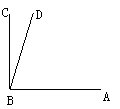
7．如图，CB⊥AB，∠CBA与∠CBD的度数比是5:1，则∠DBA＝________度，∠CBD
的补角是_________度.
8．数学课外小组的女同学占全组人数的
，加入4名女同学后就占全组人数的一半，数学课外小组原来有__________名同学
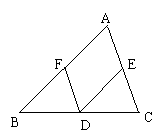9．如图∵∠CED=∠
(已知)
∴AC∥DF（ ）
10．如图∵AB∥CD(已知)
∴∠EDF=∠ （ ）
二、选择题（每小题3分，共30分）
11．－3的相反数为（ ） A.－3 B.3 C.
D.
12．代数式
表示的是（
）
A．a、b两数的差的平方与c的倒数的和 B．a、b两数的差的平方与c的相反数的和
C．a、b两数的平方差与c的倒数的和 D．a、b两数的平方差与c的相反数的和
13．互为余角的两个角之差为35°，则较大角的补角是（ ）
A．117.5° B．112.5° C．125° D．127.5°
14．已知，如图12，AB∥CD，则∠α、∠β、∠γ之间的关系为（ ）
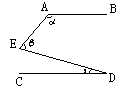A．∠α＋∠β＋∠γ＝360°
B．∠α－∠β＋∠γ＝180°
C．∠α＋∠β－∠γ＝180°
D．∠α＋∠β＋∠γ＝180°
15．如果a//b，b//c，那么a//c的依据是（ ）
A、 过直线外一点有且只有一条直线与已知直线平行
B、等量代换
C、平行于同一条直线的两直线平行
D、同旁内角互补，两直线平行
16．下列说法中错误的是（ ）
A．经过两点有且只有一条直线
B．两条直线相交，有且只有一个交点
C．经过一点，有且只有一条直线与已知直线平行
D．在同一平面内，金国一点，有且只有一条直线与已知直线垂直
17．一口井深10尺，井底有一只青蛙，当它沿着井壁往上跳时，每次可跳4尺，但要往下跌3尺，那么它跳到井口时，一共跳了（ ）
A．3次 B．7次 C．8次 D．10次
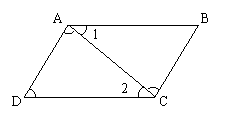18．如图，已知∠1=∠2，∠BAD=∠BCD，则下列结论
(1)AB//CD；(2)AD//BC；(3)∠B=∠D；(4)∠D=∠ACB。
其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个
19．计算机是将信息转换成二进制数进行处理的，二进制即“逢2进1”，如（1101）2表示二进制数，将它转换成十进制形式是1×23+1×22+0×21+1×20=13， 那么
将二进制数（1111）2转换成十进制形式是数 ( )
A．8 B．15 C．20 D．30
20．地球绕太阳每小时转动通过的路程约是1.1×105千米，用科学记数法表示地球一天（以24小时计）转动通过的路程约是 （ ）
A、0.264×107千米 B、2.64×106千米
C、26.4×105千米 D、264×104千米
三、解答题21．（本题5分）计算
22．（本题5分）计算
23．（本题5分）解方程：
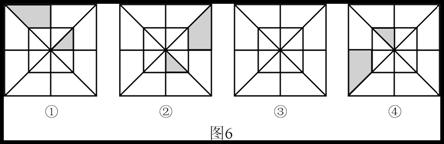
24．（本题5分）分析图6①,②,④中阴影部分的分布规律，按此规律在图6③中画出其中的阴影部分.
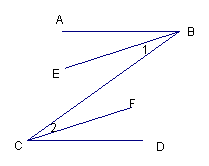
25．（本题6分）已知：如图BE//CF，BE、CF分别平分∠ABC和∠BCD
求证：AB//CD
证明：∵BE、CF分别平分∠ABC和∠BCD（已知）
∴∠1=
∠ ∠2=∠
（
）
∵BE//CF（已知）
∴∠1=∠2（ ）
∴∠ABC=∠BCD（
）
即∠ABC=∠BCD
∴AB//CD（ ）
26．（本题6分）有一些分别标有3、6、9、12 ……的卡片，后一张卡片上的数比前一张卡片上的数大3，小华拿到了相邻的5张卡片，这些卡片之和为150
（1）小华拿到哪5张卡片？
（2）你能拿到相邻的5张卡片，使得这些卡片上的数之和为100吗？
27．
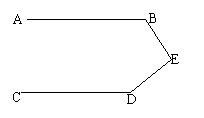（本题6分）已知：如同，AB∥CD。
根据下列语句，动手操作：(1)过点D画DF∥EB，DF与AB交于点F（画在已知图上）。
(2)求∠B+∠E+∠CDE的度数。
28．（本题6分）已知某电脑公司有A型、B型、C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元。我市某中学计划将100500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台，请你设计出不同的购买方案供该校选择，并说明理由。
29．（本题6分）甲、乙两同学做“投球进筐”游戏．商定：每人玩5局，每局在指定线外将一个皮球投往筐中，一次未进可再投第二次，以此类推，但最多只能投6次，当投进后，该局结束，并记下投球次数；当6次都未投进时，该局也结束，并记为“×”．两人五局投球情况如下：
|
| 第一局 | 第二局 | 第三局 | 第四局 | 第五局 |
| 甲 | 5次 | × | 4次 | × | 1次 |
| 乙 | × | 2次 | 4次 | 2次 | × |
（1）为计算得分，双方约定：记“×”的该局得0分，其他局得分的计算方法要满足两个条件：①投球次数越多，得分越低；②得分为正数．请你按约定的要求，用公式、表格、语言叙述等方式，选取其中一种写出一个将其他局的投球次数n换算成得分M的具体方案；
（2）请根据上述约定和你写出的方案，计算甲、乙两人的每局得分，填入牌上的表格中，并从平均分的角度来判断谁投得更好．