北师大七年级下学期数学期末试卷
班级：_______姓名：_______得分：_______发展性评语：___________
一、请准确填空(每小题3分,共24分)
1.(－2a2b)3=________;－3ab3·(－4a2b)=________;(
)－1+(3－π)0=________.
2.正方形的面积是2a2+2a+
(a＞－)的一半，则该正方形的边长为________.
3.一种病毒的长度约为0.000 052 mm,用科学记数法表示为________mm.
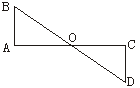
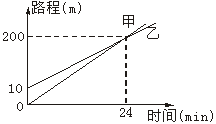
图1 图2
4.如图1所示，AC、BD相交于点O，AB＝CD，要使△AOB≌△COD,需再补充一个条件：__________.(写出一个你认为正确的即可)
5.任意写出一个两位数，个位上的数字恰好是5的概率的是________；写出一个发生概率为0的事件:________.
6.等腰三角形的底角是顶角的两倍，则此等腰三角形的顶角为________.
7.小刚正面对镜子，从镜子中看他身后的墙上写的一组数据是
,请你写出这组数据的真实数：________.
8.如图2所示，根据图中提供的信息，请你再写出三条不同的信息:_________________
__________________________________________________________________________.
二、相信你的选择(每小题3分,共24分)
9.下列各式中能用平方差公式计算的是
A.(a+b)(－a－b) B.(a+b)(－a+b)
C.(a+b)(－a－b) D.(a－b)(b－a)
10.小亮截了四根长分别为5 cm、6 cm、12 cm、13 cm的木条，任选其中三条组成一个三角形,这样拼成的三角形共有
A.1个 B.2个 C.3个 D.4个
11.在线段、角、圆、直角三角形、等腰三角形、正六边形、正五边形、四边形八个图形中，一定是轴对称图形的个数有
A.3 B.4 C.6 D.7
12.某人从甲地出发，骑摩托车去乙地，途中因车出现故障而停车修理，到达乙地时正好用了2 h.已知摩托车行驶的路程s(km)与行驶的时间t(h)之间的函数关系如图3所示.若这辆摩托车平均每行驶100 km的耗油量为2 L,根据图中给出的信息，从甲地到乙地， 这辆摩托车共耗油
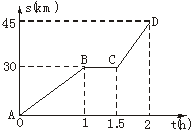
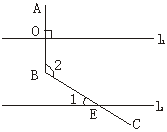
图3 图4
A.0.45 L B.0.65 L C.0.9 L D.1 L
13.如图4所示，直线l1∥l2,AB⊥l1,垂足为O，BC与l2相交于点E，若∠1＝43°,则∠2的度数是
A.43° B.47° C.120° D.133°
14.从一个箱子中摸出红球的概率为
，已知口袋中红球有4个，则袋中共有球的个数为
A.24 B.16 C.8 D.4
15.在△ABC和△A′B′C′中，AB＝A′B′,∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是
A.AC＝A′C′ B.BC＝B′C′
C.∠A＝∠A′ D.∠C=∠C′
16.如图(1),小明拿一张正方形纸片，沿虚线对折一次得到图(2),再对折一次得到图(3),然后用剪刀沿图(3)中的虚线剪去一个角再打开后的形状是
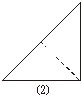
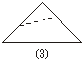
图5
图6
三、考查你的基本功(共20分)
17.(6分)计算：(1)(3x+2)－2(x2－x+2); (2)(a+b)2－(a－b)2
18.(6分)如图7,在△ABC中，高线CD将∠ACB分成20°和50°的两个小角.请你判断一下△ABC是轴对称图形吗？并说明你的理由.
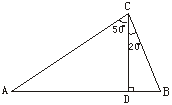
图7
19.(8分)如图8所示，△ABC中，BE⊥AD于点E，CF⊥AD于点F，且BE＝CF.根据以上信息你能得到哪些正确的结论,选一种加以说明.
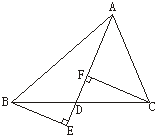
图8
四、生活中的数学(共16分)
20.(8 分)声音在空气中的传播速度y(m/s)(秒音速)与气温 x(℃)的关系，如下表.
| 气温(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)写出y与x 间的关系式；
(2)当x=150℃时，音速y 是多少？当音速为352m/s时，气温x 是多少？
21.(8 分)甲、乙两同学做摸球游戏，在口袋中装有标有1～6号数字的球(各球除号码不同外，其余全相同).游戏规定：有放回地摸球，每一轮，两人分别摸出一球，如果两球的数字之和为偶数，那么甲得 1 分；如果两球的数字之和为奇数，乙得1 分.谁先达到10分，谁就获胜.你认为这个游戏公平吗？请你给出分析结果.
五、探究拓展与应用(共16分)
22.(8 分)学校有一块等边三角形花坛，要在花坛中种上四种不同颜色的花，要求四部分的面积相等.请你在下列图中给出四种不同的设计方案.
图9
23.(8 分)有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2，
2×3×4×5+1=112=(22+3×2+1)2，
3×4×5×6+1=192=(32+3×3+1)2，
4×5×6×7+1=292=(42+3×4+1)2，
……
(1)根据你的观察，归纳发现规律，写出8×9×10×11+1的结果；
(2)试猜想n(n+1)(n+2)(n+3)+1 是哪一个数的平方？说明理由，并与同伴交流.
答案:
一、请准确填空(每小题3分,共24分)
1.(－2a2b)3=________;－3ab3·(－4a2b)=________;()－1+(3－π)0=________.
答案: －8a6b3 12a3b4 4
2.正方形的面积是2a2+2a+(a＞－)的一半，则该正方形的边长为________.
答案: a+
3.一种病毒的长度约为0.000 052 mm,用科学记数法表示为________mm.
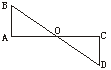
图1
答案: 5.2×10－5
4.如图1所示，AC、BD相交于点O，AB＝CD，要使△AOB≌△COD,需再补充一个条件：__________.(写出一个你认为正确的即可)
答案: ∠A=∠C(或∠B=∠D)
5.任意写出一个两位数，个位上的数字恰好是5的概率的是________；写出一个发生概率为0的事件:________.
答案: 
太阳从西方升起
6.等腰三角形的底角是顶角的两倍，则此等腰三角形的顶角为________.
答案: 36°
7.小刚正面对镜子，从镜子中看他身后的墙上写的一组数据是,请你写出这组数据的真实数：________.
答案: 85012
8.如图2所示，根据图中提供的信息，请你再写出三条不同的信息________.
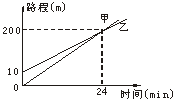
图2
答案: ①乙在甲前10 m与甲同时出发;
②甲的速度比乙的速度大;
③甲跑200 m,用时24 min,
乙跑190 m,用时24 min;
④甲跑24 min时追上乙;
⑤甲跑200 m处追上乙;
⑥200 m之前,乙在甲的前面,
200 m之后,甲在乙的前面.(任选其中三个即可)
二、相信你的选择(每小题3分,共24分)
9.下列各式中能用平方差公式计算的是
A.(a+b)(－a－b) B.(a+b)(－a+b)
C.(a+b)(－a－b) D.(a－b)(b－a)
答案:B
10.小亮截了四根长分别为5 cm、6 cm、12 cm、13 cm的木条，任选其中三条组成一个三角形,这样拼成的三角形共有
A.1个 B.2个 C.3个 D.4个
答案:B
11.在线段、角、圆、直角三角形、等腰三角形、正六边形、正五边形、四边形八个图形中，一定是轴对称图形的个数有
A.3 B.4 C.6 D.7
答案:C
12.某人从甲地出发，骑摩托车去乙地，途中因车出现故障而停车修理，到达乙地时正好用了2 h.已知摩托车行驶的路程s(km)与行驶的时间t(h)之间的函数关系如图3所示.若这辆摩托车平均每行驶100 km的耗油量为2 L,根据图中给出的信息，从甲地到乙地，这辆摩托车共耗油
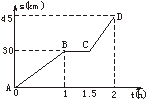
图3
A.0.45 L B.0.65 L C.0.9 L D.1 L
答案:C
13.如图4所示，直线l1∥l2,AB⊥l1,垂足为O，BC与l2相交于点E，若∠1＝43°,则∠2的度数是
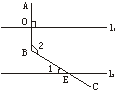
图4
A.43° B.47° C.120° D.133°
答案:D
14.从一个箱子中摸出红球的概率为，已知口袋中红球有4个，则袋中共有球的个数为
A.24 B.16 C.8 D.4
答案:B
15.在△ABC和△A′B′C′中，AB＝A′B′,∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是
A.AC＝A′C′ B.BC＝B′C′
C.∠A＝∠A′ D.∠C=∠C′
答案:A
16.如图(1),小明拿一张正方形纸片，沿虚线对折一次得到图(2),再对折一次得到图(3),然后用剪刀沿图(3)中的虚线剪去一个角再打开后的形状是
图5
图6
答案:A
三、考查你的基本功(共20分)
17.(6分)计算：
(1)(3x+2)－2(x2－x+2);
(2)(a+b)2－(a－b)2
答案: (1)－2x2+5x－2；(2)4ab.
18.(6分)如图7,在△ABC中，高线CD将∠ACB分成20°和50°的两个小角.请你判断一下△ABC是轴对称图形吗？并说明你的理由.
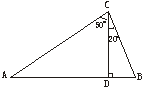
图7
答案: 是. 理由:
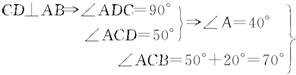
∠B=180°－∠ACB－∠A=70°
∠ACB=∠B△ABC为等腰三角形△ABC是轴对称图形.
19.(8分)如图8所示，△ABC中，BE⊥AD于点E，CF⊥AD于点F，且BE＝CF.根据以上信息你能得到哪些正确的结论,选一种加以说明.
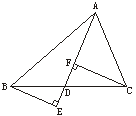
图8
答案: BD＝DC(或△BDE≌△CDF).
四、生活中的数学(共16分)
20.(8 分)声音在空气中的传播速度y(m/s)(秒音速)与气温 x(℃)的关系，如下表.
| 气温(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)写出y与x 间的关系式；
(2)当x=150℃时，音速y 是多少？当音速为352m/s时，气温x 是多少？
答案: (1)y=
x+331;
(2)当x=150℃时,y=421m/s,
当y=352m/s时,352=x+331,
x=35℃.
21.(8 分)甲、乙两同学做摸球游戏，在口袋中装有标有1～6号数字的球(各球除号码不同外，其余全相同).游戏规定：有放回地摸球，每一轮，两人分别摸出一球，如果两球的数字之和为偶数，那么甲得 1 分；如果两球的数字之和为奇数，乙得1 分.谁先达到10分，谁就获胜.你认为这个游戏公平吗？请你给出分析结果.
答案: 公平.因为每一轮摸球之后，可能有四种结果：奇数+奇数、偶数+偶数、奇数+偶数、偶数+奇数，两数的和奇、偶各占一半，而从口袋中摸到奇数和偶数球的概率也一样.所以，整个游戏公平.
五、探究拓展与应用(共16分)
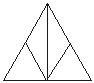
22.(8 分)学校有一块等边三角形花坛，要在花坛中种上四种不同颜色的花，要求四部分的面积相等.请你在下列图中给出四种不同的设计方案.
图9
答案: (参考)
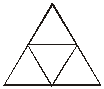
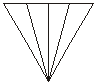
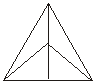
23.(8 分)有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2，
2×3×4×5+1=112=(22+3×2+1)2，
3×4×5×6+1=192=(32+3×3+1)2，
4×5×6×7+1=292=(42+3×4+1)2，
……
(1)根据你的观察，归纳发现规律，写出8×9×10×11+1的结果；
(2)试猜想n(n+1)(n+2)(n+3)+1 是哪一个数的平方？说明理由，并与同伴交流.
答案: (1)8×9×10×11+1=892=(82+3×8+1)2；
(2)n(n+1)(n+2)(n+3)+1=(n2+3n+1)2.
理由:n(n+1)(n+2)(n+3)+1
=(n2+3n+2)(n2+3n)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2.