6.1.1 有序数对 班级 座号 姓名
1.在电影院内，确定一个座位一般需要 个数据，其理由 ；
2.七年级⑵班座位有七排8列，张艳的座位在2排4列，简记为（2，4），班级座次表上写着王刚（5，8），那么王刚的座位在
；
3.如图1，圆的直径为4cm，如点C的位置在点O的东南方向，距O
点2cm，那么点B的位置在点O的 ；
4.如图2，若用（0，0）表示点A的位置，试在方格纸中标出B（2，4），
C（3，0），D（5，4），E（6，0），并顺次连接起来，是英文字母中的 ；
5.如图3，若D（2，0），则A、B、C点可表示为 ；
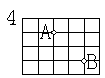
6.如图4，若A的位置是（6，3），则B的位置可表示为
（ ）
A、（7，4） B、（5，7）
C、（8，4） D、（8，5）
快乐晋阶
8.如图，六角星的顶点A的位置用（6，－3）表示，那
么请写出其他五个顶点的位置；如果顶点A的位置用
（0，0）表示，你能写出其他五个顶点的位置吗？
如果能，请确定其他五个顶点的位置。
9.如图，某校的部分平面示意图，借助刻度尺和量角器看图填空：⑴图书馆位于桃李亭的方位角是
，到桃李亭的图上距离约为 cm；⑵如果用（2，4）表示图上桃李亭的位置，那么综合楼的位置表示为
；（6，8）表示为
，（7，1）又表示校园内某个地方，它是
。
 |
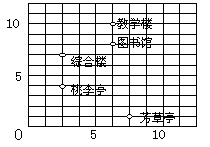10.如图5，如果用（0，0）表示O点的位置，那么图中的A、B、C的位置如何表示？
（7，8），（7，10）分别表示图中的哪个点？
 |
11.七年级⑴的小芳、小明、小亮、小新与学校的大致
位置如图，若一个小正方形的边长表示0.5km，
试用不同的方法表示小芳、小明、小亮、小新家相
对于学校的位置。
12.如图，是小明家和学校所在地的简单地图，已知OA=2cm，OB=2.5cm，OP=4cm，C为OP的中点，
回答下列问题：⑴ 图中距小明家距离相同的是那些地方？
⑵ 商场、学校、公园、停车场分别在小明家的什么方位？哪两个地方的方位是相同的？
⑶ 若学校距离小明家400m，那么商场和停车场分别距离小明家多少m？ 北
 |
6.1.2 平面直角坐标 班级 座号 姓名
轻松入门
1.在平面内，两条 的数轴组成平面直角坐标系；
2.两条数轴通常分别置于 位置与 位置，取 与 的方向分别为两条数轴的正方向，水平的数轴叫做 或 ,竖直的数轴叫做 或 ，其交点O称为 ；
3.平面直角坐标系内有一点P（x，y），若点P在横轴上，则 ，若点P在纵轴上，则 ，坐标原点O的坐标是 ；
4.点A（2，7）到x轴的距离为 ，到y轴的距离为 ；
5.在平面直角坐标系中，点A的位置为（－3，2），B的位置为（3，2），连接A、B两点所成线段与 平行；
6.若点（a＋5，a－2）在y轴上，则N点的坐标为 ；
7.已知点P在第二象限，它的横坐标与纵坐标的和为1，点P的坐标可以是 ；（写一个即可）
8.若平面直角坐标系中线段MN所在的直线是x轴正方向与y轴正方向所成角的平分线，且 M（4，a），
N（b，2），则a = ，b = ；
9.已知A（3，2），AB∥x轴，则B点的坐标为 ；
10.如图，六边形ABCDEF各个顶点的坐标依次
为
11.若点P（a，b）在第四象限内，则a，b的取值范围是 （ ）
A、a＞0，b＜0 B、a＞0，b＞0
C、a＜0，b＞0 D、a＜0，b＜0
12.如果点A（x，y）在第三象限，则点B（－x，y－1）
在 （ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
13.点P（－3，4）到y轴的距离是 （ ）
A、3 B、4 C、－3 D、5
14.在平面直角坐标系中，依次描出下列各点，并将各组内的点依次连接起来：⑴（2，1），（2，0），
（3，0），（3，4）；⑵（3，6），（0，4），（6，4），（3，6）。你发现所得的图形是 （ ）
A、两个三角形 B、房子 C、雨伞 D、电灯
15.如图，人头左边嘴角的坐标是 （ ）
A、 （1，－1） B、（－3，－1）
C、（－1， 1） D、（－1，－3）
16.点P位于y轴左方，距y轴3个单位长，位于x轴上
方，距x轴4个单位长，点P的坐标是 （ ）
A、（3，－4）B、（－3，4） C、（4，－3）D、（－4，3）
17.已知点P（x，y）在第二象限，且
，
则点P的坐标为
（ ）
A、（－3，5）B、（1，－1）C、（－3，－1）D、（1，5）
18.如图，已知：A（3，2），B（5，0），E（4，1），
则△AOE的面积为 （ ）
19.在平面直角坐标系中描出下列各组点，并将各组的点
用线段依次连接起来：
⑴（0，0），（1，3），（2，0），（3，3），（4，0）
⑵（0，3），（1，0），（2，3），（3，0），（4，3）
观察所得的图形，你觉得像什么？
 |
20.如图，建立两个不同的平面直角坐标系，在每个平面
直角坐标系中，分别写出8个角的顶点的坐标，并比较
同一顶点在两个坐标系中的坐标。
 |
21.如图，写出图中点A、B、C、D、E、F、G、H的坐标，
并观察点A和C，点B和D有什么关系？在图中标出
（－2，4）、（5，5）、（4，－3）三点的位置。
22. ⑴ 画出A（5，7），B（2，3），C（5，3）为顶点的△ABC，并求其面积；
⑵ 画出A（0，0），B（5，0），C（1，4），D（6，4） 为顶点的四边形ABCD，并求其面积。
23.如图，正方形ABCD边长为10，连结各边中点E、F、
G、H得正方形EFGH，建立适当得直角坐标系，分别
写出A、B、C、D、E、F、G、H的坐标？
生活拓展
24.如图，在平面直角坐标系中，已知A（3，2），B（0，0），C（4，0），
在坐标系内找一点D使A、B、C、D四点构成一个平行四边形。