七年级数学上期目标检测题
八、 可能性
（时间：90分钟 总分：100分）
班级 _ 姓名______ 学号 成绩
一、填空（每小题3分，共10分）
1、A表示必然事件，B表示不可能事件，C表示不确定事件，在下列事件后填上表示事件类型的字母。
（1）明天是晴天 （ ）
（2）54人中有两人的生日相同 （ ）
（3）今天星期一，明天星期二 （ ）
（4）明年有370天 （ ）
（5）打开电视正在播广告 （ ）
（6）掷一次骰子，6点朝上 （ ）
2、小虎用瓶盖设计了一个游戏：任意掷一个瓶盖，如果盖面朝上则甲胜，如果盖口朝上则乙胜。你认为这个游戏（ ）。（填“公平”或“不公平”）
3、一个不透明的口袋中着大小、外形等一样的5个红球，3个蓝球，2个白球，搅匀后，请判断下列事件：（填番号）
（1） 从口袋中任取5个球是白球
（2） 从口袋中任取5个球全是蓝球
（3） 从口袋中任取5个球，只有蓝球和白球，没有红球。
（4） 从口袋中任取9个球，则红、蓝、白三种颜色的球全齐了。
其中不确定事件有（ ），不可能事件有（ ），必然事件有（ ）。
4、请各举一例
（1）必然事件： （ ）
（2）不可能事件：（ ）
（3）不确定事件：（ ）
5、在转盘游戏中，红、蓝和白色三个区域扇形的圆心角之比为3∶2，则指针落在（ ）区域的可能性大。
6、任意翻一下日历，（ ）翻出2月3日。（填“不太可能”或“很可能”）
7、同时随机抛掷2枚硬币，所有可能发生的事件有（ ）种，它们是（ ）。
8、掷一枚均匀的骰子，骰子的每个面上分别标有数字1，2，3，4，5，6，则“6”朝上的可能性为（ ），偶数朝上的可能性为（ ），3的倍数朝上的可能性为（ ）。
9、一个口袋中装有4个红球，3个白球，至少摸出（ ）个球，才能保证其中有红球。
10、写1~9个数字组成9张卡片，从中任意抽出4张能够组成的最大四位数是（ ），得到这个四位数的可能性是（ ）。
二、 选择题（每小题3分，共15分）
11、某城市有10000辆自行车，其牌照编号为00001~10000，问某人在路上偶然遇到一辆自行车，其牌照号码大于9000的可能性是（ ）
A、
B、
C、
D、
12、在一个口袋中有20只除颜色外，其他完全相同的球，若任取一只为红球的概率为3/4，则其中红球有（ ）个。
A、12 B、15 C、18 D、14
13、甲班有64名学生，他们的座号从1~64号，任意抽问一个同学，他的座位号大于32的可能是（ ）
A、
B、
C、
D、
14、随机地掷一枚质地均匀的正方体骰子 ，下面几个可能发生的事件中，可能性较大的是（ ）
A、点1朝上 B、点1或6朝上 C、3的倍数朝上 D、2的倍数朝上
15、随意投掷三次硬币，三次均是国徽朝上的可能性是（ ）
A、
B、
C、
D、
三、 解答题（共24分）
16、（8分）现有10张卡片，它们大小、形状、背面完全一样，在正面5张写有数字“1”，有2张写有数字“5”，有2张写有数字“4”，有一张写有数字“2”，若用P表示每种情况的可能性，
求：（1）P（摸“1”号卡片）， （2） P（摸“2”号卡片），
（3）P（摸奇数卡片）， （4）P（摸质数卡片）
17、（8分）袋子里有3个白球，3个红球，4个黄球共10个球，每个球除颜色外都相同，从中任意摸出一球，若用P表示相应事件发生可能性的大小，求： （1） P（摸到红球）， （2） P（摸到白球）， （3）P（摸到黄球）， （4） P（摸到的不是白球）
18、（8分）请用“不可能”、“不太可能”、“可能”、“很可能”、“必定”等语言描述下列事件的可能性：
（1）王红的身高达5米 ____________
（2）将一个普通玻璃杯用力摔到水泥地上，玻璃杯破了 ___________
（3）袋中有9个球，4个黑球，5个白球，从中任意摸一个球，摸到白球 _________
（4）小明将朋友家里的电话号码忘记了，他随意输几个数字，电话通了，正好是朋友家。 __________
（5）100个红球，1个白球，从中任意摸1个，恰好摸到红球。 __________
四、解答题：（31分）
19、（8分）有如下三幅图：将它们混在一起背面朝上，一次抽取两张，若是两个三角形，可拼成平行四边形；若一个三角形与一个正方形，可拼成小房子。问出现平行四边形的可能性与出现小房子的可能一样大吗？说明理由。
 |
20、（7分）如图，在自由转动的转盘中，A、B、C、D四个扇形的圆心角度数为180度、60度、30度、90度。当转盘停止转动时：
（1）
 |
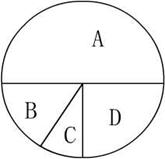用语言描述指针分别指向A、B、C、D的可能性大小。
（2） 分别求出指针指向A、B、C、D的大小。
| |
（1）主人一次就打开密码箱的可能性P1是多少？
（2）若主人想起第一个数码是3，那么试一次就打开密码箱的可能性P2是多少？
（3）若主人想起第一个数码是3 ，并且想起第二个数码为奇数，且大于5，那么试一次就打开密码箱的可能性P4是多少？
21、设计一个有红、黄两种颜色的转盘，使得指针转到红颜色的概率为。至少写出三种设计方案。
23、（8分）先后抛掷两枚均匀的硬币。 （1）共可能出现多少种不同的结果？ （2）出现“1枚正面、1枚反面”的结果有多少种？ （3） 求出现“1枚正面、1枚反面”的概率是多少时，有人说：“一共可能出现‘2枚正面’、‘2枚反面’、‘1枚正面、1枚反面’这3种结果，因此出现‘1枚正面、1枚反面’的概率是，这种说法对不对？为什么？ （4）设计一种游戏：两枚同面则甲胜，两枚异面则乙胜，你认为这种游戏公平吗？
24、某同学发明了一个素数乘法游戏，抛掷两个各面标有1，2，3，4，5，6的均匀的骰子 ，用两次朝上的点数相乘，得到一个乘积，如果乘积是素数，玩家A得10分，如果乘积不是素数，玩家B得1分，由于得到非素数积的抛掷方式要比得到素数积的抛掷方式多得多，该同学自认为游戏是公平的。你认为如何？做一做这个游戏，检验它是否公平。