初一下数学期末复习（八） 班级____姓名____
一、耐心填一填（每空2分，共34分）
1、若2x3－2k＋3k=1是关于x的一元一次方程，则k= ____,方程的解为__________;
2、一个正多边形的内角和等于1080°，它的边数是______,每个内角是________°.
3、不等式－4x≥－12的正整数解为
不等式组
的解集是 ________．
4、若a＞b，则a－（－c） b－（－c）;当x＜1时－3x＋3 0
5、用正三角形和正方形能够镶嵌地面，已知每个顶点周围有x个正三角形y个
正方形，则x+2y=_________。
6、若等腰三角形的一个角是另一个角的2倍，则它的底角是 ______，
该三角形的对称轴是 。
|
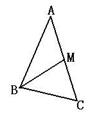如图，BM是△ABC中AC边上的中线，AB=5cm，BC=3cm， 那么△ABM与△BCM的周长之差______cm.
8、若x－y－3＋(2x＋3y－6)2=0，则x＋y= ；
|
n－7=_______
10、如图，在ΔABC中，∠A=28°，∠B=60°，CD⊥AB于D，
CE平分∠ACB，则∠ECD的度数为 。
11、甲、乙两商店某种铅笔标价都是一元，学生小王欲购买这种铅笔，发现甲、乙两商店都让利优惠，甲店实行每买5枝送一枝(不足5枝不送)；乙店实行买4枝或4枝以上打8.5折，小王买了13枝这种铅笔，最少需花___________元。
12．如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=50°，则∠BDF的度数是_________
二、精心选一选（每小题2分，共22分）
13、若代数式7—2x和5—x的值互为相反数，则x的值为（ ）
A
4 B 2 C 
D 
14、不等式组
有解，
的取值范围是（ ）
A、
B、≥8 C、
D、≤8
15、不等式组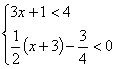
的最大整数解是（ ）
A、0 B、－1 C、－2 D、1
16、四张完全相同的卡片上，分别画有圆、平行四边形、等边三角形、30°的角，现从中随机抽取一张，卡片上画的恰好是轴对称图形的机会为（ ）
A．
B． C．
D．1
17、下列图形中一定能拼成一个等腰直角三角形的是( )
A．两个等腰三角形 B．两个可重合的等腰三角形
C．两个可重合的等腰直角三角形 D．两个可重合的等边三角形
18、二元一次方程2x＋y=5的正整数解为----------------------------------- -（ ）
A．
B．
C．或 D．以上都不对
19、等腰三角形的两边长分别为4cm、7cm，则这个三角形的周长为-（ ）
A．15cm B．18cm C．15cm或18cm D．不能确定
20、小亮在镜中看到身后墙上的时钟如下, 你认为实际时间最接近8:00的是 ( )
A. B. C. D.
21. 为保护生态环境，陕西省某县响应国家“退耕还林”号召，将某一部分耕地改为林地，改变后，林地面积和耕地面积共有180平方千米，耕地面积是林地面积的25%，为求改变后林地面积和耕地面积各多少平方千米。设改变后耕地面积x平方千米，林地地面积y平方千米，根据题意，列出如下四个方程组，其中正确的是（
）A
B
C
D
22．设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列四个图中，能表示它们之间关系的是 （ ）。
 |
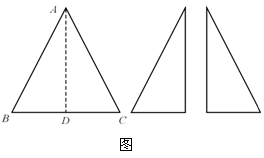
23．如图，已知BC为等腰三角形纸片ABC的底边，AD⊥BC，AD=BC. 将此三角形纸片沿AD剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出互不相同的四边形的个数是 ( ) A.
1 B.
2 
C. 3 D. 4
三、用心想一想
24、计算（每小题3分，共12分）
（1）3x＋7=1＋2x （ 2）
(3)
（4）
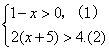（并将解集在数轴上表示出来）
25、如果关于x、y的二元一次方程组
的解是
，那么关于m、n的方程组
的解是多少（仔细观察两方程组的特点并思考，本题可有简单方法哟！）（5分）
26、一辆汽车在直线型的公路AB上由A向B行驶M、N分别是位于公路AB两侧的村庄，汽车行驶到哪一点时，与村庄M、N的距离相等？请在图上找到这一点。（不写作法，保留作图痕迹）（3分）
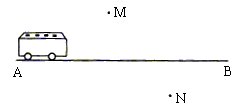
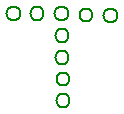
27、如图是小明用棋子摆成的字母“T”，它的主要特点是轴对称图形.请你再用棋子摆出两个轴对称图形的字母（用O代表棋子）（4分）
28、概率论起源于赌博，据传意大利的业余数学家卡当就曾热衷于赌博，试图研究赌博不输的方法。卡当曾参加过这样一次赌博：把两个骰子掷出去，以每个骰子朝上的点数之和作为赌的内容，那么你认为卡当把赌注下在几点最有利呢？并说明理由。(4分)
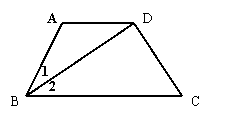
29如图，已知AD//BC，∠1=∠2，∠A=112°，且BD⊥CD，求∠ABC和∠C的度数（5分）
 |
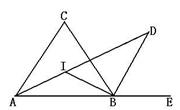
30阅读以下材料，回答问题：（6分）
如图a，△ABC中，AI、BI分别是△ABC中∠BAC和∠ABC的
平分线，
|
分线，交AI的延长线于
D.试探求∠AIB、∠C、∠D三角之间的两两关系式.探究：
⑴若∠CAB＝46°，∠ABC＝72°，试求∠C、∠AIB、∠D的大小
⑵由BI、BD分别是△ABC中∠ABC的内角和外角平分线，可得如图b
的基本图形，由此图形得，∠DBI＝_________°，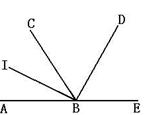
在△DBI中，∠AIB是
外角，所以∠AIB＝_________ _ . (写出与∠D的关系式)
⑶猜想：①∠AIB与∠C的关系式：_______________________； (b)
②∠D与∠C的关系式： _______________________.
⑷任意选取⑶中一个关系式证明之，并利用它结合⑵中的结论推出另一个关系式.
31．我校本学期前三周每周都组织初三年级学生进行一次体育活动，全年级400名学生每人每次都只参加球类或田径类中一个项目的活动．假设每次参加球类活动的学生中，下次将有20%改为参加田径类活动；同时每次参加田径类活动的学生中，下次将有30%改为参加球类活动．（5分）
⑴如果第一次与第二次参加球类活动的学生人数相等，那么第一次参加球类活动的学生应有多少名？
⑵如果第三次参加球类活动的学生不少于200名，那么第一次参加球类活动的学生最少有多少名？