初一平行班数学试卷
说明:同学们,请注意无特殊注明的题全体同学都必须解答;标为“(B层必做)”的题为考B卷同学的必答题;标为“(A层必做)”的题为考A卷同学的必答题,不得交叉答题,否则,该题以零分计算!
一、 判断题:(1,×5=5)
1、两直线被第三直线所截同位角相等。 ( )
2、三角形的中线就是过顶点平分对边的直线。 ( )
3、三角形的高就是顶点到对边的距离。 ( )
4、![]() ( )
( )
5、一个多边形最多有3个锐角。 ( )
二、选择题:(3,×9=27)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 答案 |
1、下列运算中正确的是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、在一个三角形中,若∠A=∠B=450 ,则△ABC是 ( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上都不对
3、若![]() ,则 m的值等于( )
,则 m的值等于( )
A、4 B、6 C、7 D、8
4、下列长度的三根木棒首尾相接,不能做成三角形框架的是( )
A、5cm、7cm、10cm B、7cm、10cm、13cm
C、5cm、7cm、13cm D、5cm、10cm、13cm
5、![]() 等于 ( )
等于 ( )
A、![]() B、
B、![]() C、
C、 ![]() D、
D、![]()
6、若两条平行线被第三条直线所截,则同一对同位角的平分线互相( )
A、垂直 B、平行 C、重合 D、相交
7、平移改变的是图形的( )
A、位置 B、大小 C、形状 D、位置、形状、大小
8、(B层必做)一个多边形的边数每增加一条,这个多边形的( )
A、内角和增加3600 B、外角和增加3600
C、对角线增加一条 D、内角和增加1800
(A层必做)下列哪个度数可能成为某个多边形的内角和( )
A、2400 B、6000 C、19800 D、21800
9、(B层必做)-27![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、-
D、-![]()
(A层必做)已知![]() ,那么
,那么![]() 的正确结果是 ( )
的正确结果是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、填空题:(2,×12=24)
1、如图1,能判定DE∥BC的同位角有 组。
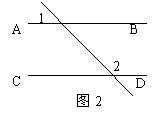
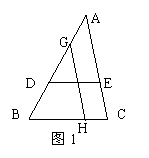 2、如图2,AB∥CD,若∠2是∠1的2倍,则∠2= 。
2、如图2,AB∥CD,若∠2是∠1的2倍,则∠2= 。
 |
3、把字母“E”平移需要知道 个关键点。
4、一个五边形有三个内角是直角,另两个内角的度数都等于X,
则X的值为:
5、(B层必做)已知三角形的两边长是3和4,周长是整数,则这样的三角形
共有 个。
(A层必做)已知三角形的两边长是3和4,周长是偶数,则这样的三角形
的第三边是 。
6、(B层必做)若![]() ,
,![]()
若![]()
(A层必做)已知![]() ,则(1)
,则(1)![]()
(2)![]() (3)
(3)![]()
7、如图3。D、E、F在△ABC的边BC上,若∠1=∠2=∠3=∠4,则AF是△
的角平分线, 是△ABC的角平分线,若∠BAC=1000,
则∠DAF= 0
 | |||
 | |||
8如图4,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是BC的三倍,则图中四边形ACED的面积为
四、计算题:(4×4=16)
1、![]() 2、
2、![]()
3、若![]() ,求 x+y 4、
,求 x+y 4、![]()
五、解答题:(4,×5+8,×1=28)
1、(B层必做)在四边形ABCD中,∠A、∠B、∠C、∠D之比是3∶4∶5∶6,
求四边形各内角的度数。
(A层必做)在四边形ABCD中,∠A、∠B、∠C、∠D的外角之比是8∶6∶3∶7,
求四边形各内角的度数。
2、如图5,△ABC中,∠ACB=900,CD⊥AB于D,若AC=4cm,BC=3 cm,AB=5 cm;
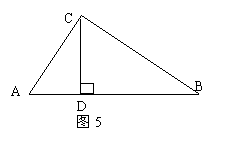 求线段CD的长。
求线段CD的长。
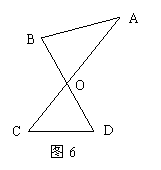
3、(B层必做)如图6,AC、BD交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
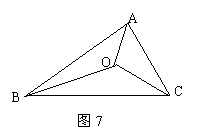 (A层必做)如图7,O为ABC内一点,请比较OA+OB+OC与
(A层必做)如图7,O为ABC内一点,请比较OA+OB+OC与![]() (AB+BC+AC)的大小,并说明理由。
(AB+BC+AC)的大小,并说明理由。
4、若两个多边形的边数之比为1∶2,两个多边形的内角和为14400,求这两个多边形的边数。
5、将长度为24的一根铝丝折成各边为均为正整数的三角形,这个三角形的三边分别记为a、b、c,且a≤b≤c,请尽可能地写出满足题意的a、b、c。
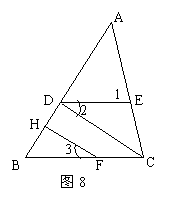 6、如图8,已知∠1=∠ACB,∠2=∠3,FH⊥AB于H,
6、如图8,已知∠1=∠ACB,∠2=∠3,FH⊥AB于H,
求证:CD⊥AB
证明:∵∠1=∠ACB ( )
∴DE∥ ( )
∴∠2= ( )
∵∠2=∠3 ( 已知 )
∴∠3=∠ ( )
∴CD∥ ( )
∴∠BDC=∠ ( )
又∵FH⊥AB ( )
∴∠BDC=∠ = 0
∴ ( )