七年级下期中学数学期中考试题
(全卷共三个大题，30个小题，满分150分，120分钟完卷)
一. 选择题：(本大题共12个小题，每小题4分,共48分)在每个小题的下面，都给出了代号为A.B.C.D的四个答案，其中只有一个答案是正确的，请将正确答案的代号填在答题卷上。
1.已知
那么x-y的值是（ ）
A. 1 B. ―1 C. 0 D. 2
2. 一个多边形的内角和比它的外角和的3倍少180
，则这个多边形的边数是（
）
A．5 条 B. 6条 C.7 条 D.8条
3. 已知等腰三角形的两边分别为6 cm, 3cm, 则三角形周长是（ ）
A．9cm B .12cm C.12cm 或 15 cm D.15cm
4如果点P(m+3,m+1)在直角坐标系的X轴上，则P点坐标为（ ）
A.(0,2) B.(2,0) C.(4,0) D.(0,-4)
5. 直角坐标系中, 已知点A (0,0) ,B(2,0) ,C(3,4) ,D(1,4) 顺次连接A,B,C,D, 则四ABCD是( )
A.平行四边形 B.长方形 C.正方形 D.梯形
6. 如果点 A的坐标为（a
+1 , -1-b）,那么点A在（ ）
A.第一象限 B. .第二象限 C. 第三象限 D. 第四象限
7. 已知a+2b-9+(3a-b+1)=0 ,则a+b的值为（ ）
A. 3 B. 4 C. 5 D. 5
8. 如果点(2x,x+3)在X轴的上方,Y轴的右侧,且该点到X轴与Y轴的距离相等,则x的值为( )
A.1 B.-1 C.3 D.-3
9. 方程x+2y=7在自然数范围内的解（ ）
A.只有1个 B.有无数个 C.只有3个 D.只有4个
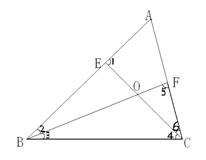
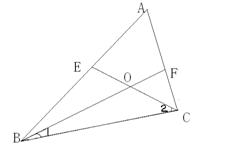
10. 如图，已知∠ABC和∠ACB的角平分线BD,CE相交于点 O, ∠A=50，则∠BOC的度数为（
）
A.110
B.115
C.120
D.125
|
（第10题） （第11题）
11. 如图，∆ABC中，点E,F分别在AB,AC上，则下列各式中不成立的是（ ）
A．∠BOC=∠2+∠6+∠A, B. ∠2= ∠5-∠A, C. ∠5=∠3+∠1, D. ∠11=∠ABC+∠4 。
12. 方程mx+ny=10的解是
及
则3m+7n=( )
A.100 B.101 C.102 D.103
二. 填空题:( 本大题共10个小题，每小题3分,共30分). 请将答案直接填写在答题卷对应的横线上。
13.已知
是方程 2x+ay=5的解，则a=____________
14. 一个多边形的每个外角都是45，那么这个多边形的内角和为____________。
15.三角形三个外角之比为2：3：4，则与之相应的三个内角之比为_________________。
16．点P(2,5) 关于X轴对称的点的坐标是___________,关于Y轴对称的点的坐标是___________,关于原点对称的点的坐标是___________。
17．如果 3x+2+2y-1 =0, 那么点P(x,y) 在第_____象限，Q(x+1,y-2)在第_____象限。
18．坐标原点 O(0,0) , A(-2,0) , B(-2,3) 三点围成的∆ABC的面积为_______________。
19. 已知线段AB=3, AB // X轴,若点A的坐标为 (1,2) ,则点B的坐标____________。
20．已知三角形ABC, A(-3,2), B(1,1), C(-1,-2), 现将∆ABC平移，使点A到位置A’(1，-2)处，则点B,C对应的坐标分别为 B’（__________）,C’（_________）。
|
|
|
（21题） （22题）
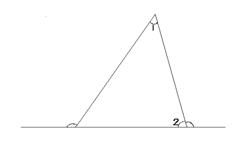
22. 如图，∠
=125，∠1=50,则∠
的度数是___________ 。
三. 解答题:( 本大题共8个小题，每小题9分，共72分)下列各题解答时必须写出必要的演算过程或推理步骤，并将解答过程写在答题卷上。
23．平面直角系内有四个点A(1,2), B(-2,1), C(0,-1), D(2,0), 顺次连接A,B,C,D,求四边形ABCD的面积？
24．等腰三角形一腰上的中线把该三角形的周长分为13.5cm和 11.5cm 两部分，求这个等腰三角形各边长。
25．已知ΔABC中，三边长是a,b,c,都是整数，且满足a>b>c, a=8, 那么满足条件的三角形共有多少个？
26.已知方程（2m－6）x
+(n+2)y
=0是二元一次方程，求m , n 的值。
27.方程组
的解适合方程x+y=2 ,求代数式m–2m+1的值。
28.甲．乙两人共同解方程组
由于甲看错了方程（1）中的a 得到方程组的解为
，乙看错了方程（2）中的 b ，得到方程组的解为
，试计算 a
+(―
b)
的值。
29．某中学新建了一幢4层的教学大楼，每层楼有8间教室，进出这幢大楼共有4道门，其中两道正门大小相同，两道侧门大小也相同，安全检查中，对4道门进行了测试，当同时开启一道正门和两道侧门时，2分钟内可以通过560名学生；当同时开启一道正门和一道侧门时，4分钟内可以通过800名学生。
（1） 问平均每分钟一道正门和一道侧门各可以通过多少名学生？
（2） 检查中发现，紧急情况时因学生拥挤，出门的效率将降低20%，安全检查规定，在紧急情况下，全大楼的学生应在5分钟内通过这4道门安全撤离，假设这幢教学大楼每间教室最多有45名学生，问这4道门是否符合安全规定？请说明理由。
30．如图，已知
中，∠B >∠C ，AD为∠BAC的角平分线，AE ⊥ BC,垂足为E ,试说明∠DAE =
(∠B -∠C) .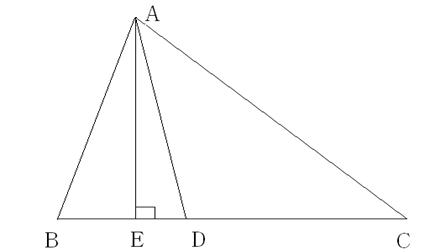 
(30题)