七年级下数学期末复习(一)班级___姓名__
一、细心填一填(每空2分,共36分)
1、 已知x=4是关于x的方程ax-5=4+a的解,则a=
2、 不等式-3x-10<0的负整数解有 个
3、 一个正多边形的每个内角为135°,则它是正 边形
4、 关于x的方程2x-2m=x-2的解是非负数,则m的取值范围是
5、 一副三角板按如图(1)叠放在一起,则图中的∠1的度数是
6、 根据图(2)中所提供的信息,可知每一支网球拍的单价是 每一块乒乓球拍的单价是
7、  某种药品的说明书上贴有如图(3)所示的标签,请用不等式解集的形式表示一次服用这种药品的剂量(x) 的取值范围
某种药品的说明书上贴有如图(3)所示的标签,请用不等式解集的形式表示一次服用这种药品的剂量(x) 的取值范围
8、 已知(2x+y+10)2与![]() 互为相反数,则x+y=
互为相反数,则x+y=
9、 过多边形的某个顶点的所有对角线,将该多边形分成9个三角形,则这个多边形的内角和为
10、中央电视台“开心辞典”栏目中有这样一个问题:10个连续自然数按从小到大的顺序依次排列,前5个数的和为70,则这10个数中最后一个数是
11、请在后面的横线上写一个关于x、y的二元一次方程,使所组成的方程组的解满足方程x+2y=0(只要写出一个满足题意的即可但不能写题目中已有的两个方程):![]()
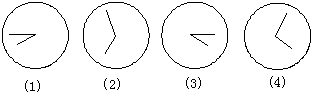
 12、小刚从镜子中看到挂在他身后墙上的四个时钟如图(4)所示,其中时间最接近8点钟的是 (填编号)
12、小刚从镜子中看到挂在他身后墙上的四个时钟如图(4)所示,其中时间最接近8点钟的是 (填编号)
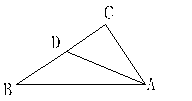
13、如图(5),在△ABC中,∠C=90°,AD平分∠BAC,BC=8,BD-DC=2,AB=10,则:△ABD的面积为 ,AC=
| x | -1 | 0 | 1 | 2 | 3 |
| y | 4 | 2 | 0 | -2 | -4 |
14、已知不等式组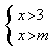 的解集是x>3,则m的取值范围是
的解集是x>3,则m的取值范围是
15、已知关于x、y的二元一次方程ax+b=y(其中a、b是常数),x与y的部分对应值如表:,根据以上所提供的信息可得:关于x的方程ax+b=0的解是,关于x的不等式ax+b>0的解集是
二、精心选一选(每题2分,共16分)
16、如果a<b,则下列结论正确的是( )
A. ac<bc
B. ac2<bc2 C. -3+a<-3+b D. ![]()
17、如果一个三角形的两个内角的角平分线所成的钝角是135,则这个三角形的形状为( )
A. 锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
18、下面有4个汽车标致图案,其中是轴对称图形的是( )
 A、②③④ B、①③④ C、①②④ D、①②③
A、②③④ B、①③④ C、①②④ D、①②③
19、小颖设计了如下四中正多边形的瓷砖图案,在这四种瓷砖中,可以用单独一种瓷砖铺满墙面的是( )
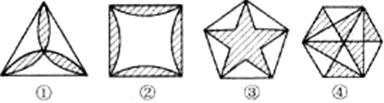
A. ①②④ B.②③④ C. ①③④ D. ①②③
20、有一个商店把某种商品按进价加30%作为定价,可是总卖不出去;后来老板按定价减价30%以182元出售,很快就卖掉了,则这次生意的盈亏情况为
A. 赚18元 B. 亏78元 C. 亏18元 D.不赚也不亏
21、用足够多的长为4cm和8cm的两种小木棒可搭成多少种不同的等腰三角形的木架(不允许截取木棒)( )
A. 1种 B. 2种 C. 3种 D.以上答案都不对
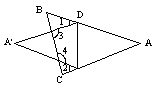 22、如图所示,把一张三角形纸片ABC沿着DE折叠,点A落在点A′处,则下列结论错误的是( )
22、如图所示,把一张三角形纸片ABC沿着DE折叠,点A落在点A′处,则下列结论错误的是( )
A. DE是线段AA′的垂直平分线
B.∠3+∠4+2∠A=360°
C.∠1+∠2=2∠A′
D.若∠1=∠2,则EA′∥AB
23、无锡教育电视台在某个周末的黄金时段的3分钟内插播长度为20秒和40秒的两种广告,20秒的广告每次收费6000元,40秒的广告每次收费10000元。若要求每种广告播放不少于2次,那么电视台在这一天晚上的黄金时段的3分钟内插播广告可获得的最大收益是( )A. 48000元 B. 50000元 C. 52000元 D. 54000元
三、用心答一答((第24题16分,第25、26、27题各6分,28、29题各7分,共48分)
24、解方程(组)或不等式(组)
(1)![]() (2)
(2)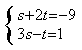
(3)![]() (4)
(4)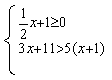
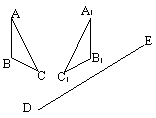
25、如图,△ABC和△A1B1C1 关于直线MN对称,
(1)请画出直线MN;(2)画△A2B2C2,使它与△A1B1C1关于直线DE对称;
(3)设直线MN与直线DE交于点O,它们所夹的锐角为60°,则通过探究可知:∠COC2
= 度。(只要填写结果即可)
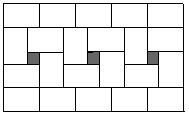
26、同样大小的长方形小纸片摆成如图的图形,中间形成了三个小正方形的空隙(图中阴影部分),已知小纸片的宽(较短边)为12cm,(1)求长方形小纸片的长及小正方形的边长;(2)现要用7块这样的长方形小纸片拼成一个既不重叠也没有空隙的大长方形,请设计出两种不同的方法,画出示意图(要求所拼成的大长方形的较长边不超过52cm)。
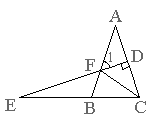
27、如图,△ABC中,∠ABC=∠C,DE⊥AC于点D,交AB于点F,交CB的延长线于点E,连接CF。
(1)设∠E=m°,试用含m的代数式表示∠1的度数;
(2)若点D是AC的中点,AB+BC=5,那么图中哪一个三角形的周长可求出来?是多少?
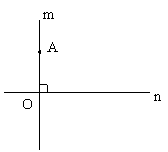
28、如图,m、n分别是两条互相垂直的直线,垂足为点O,点A在直线m上,且OA=40厘米,P、Q两点分别在直线m、n上作匀速运动,其中,点P从点A开始以每秒5厘米的速度向下运动,点Q从点O开始以每秒3厘米的速度向右运动,且P、Q两点同时出发。
(1)几秒钟时,△PQO是等腰三角形?(2)是否存在这样的时刻,使得点Q与点A、P的距离相等?若存在,求出这个时刻,若不存在,说明理由。
29、为了美化无锡,创建文明卫生城市,无锡市园林局决定利用现有的2600盆甲种花卉和1780盆乙种花卉搭配A、B两种园艺造型共40个,摆放在市民广场的两侧。已知搭配每个造型所需花卉情况如下表所示,综合上述信息,解答下列问题:
| 造型 | 甲 | 乙 |
| A | 80 | 20 |
| B | 30 | 90 |
(1)符合题意的搭配方案有几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1200元,试说明选用(1)中哪种方案成本最低?