七年级下学期期末数学试卷
一、选择题（每小题3分，共30分）
1．下列各式不是单项式的是（ ）．
A．4x2 B．a C．－1
D．5m —1
2．一个角的度数是40°，那么它的余角的度数是（ ）．
A．60° B．140° C．50° D．90°
3．如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，
使其不变形，这样做的根据是（ ）．
A．两点之间的线段最短
B．长方形的四个角都是直角
C．长方形是轴对称图形 （第3题图）
D．三角形有稳定性
4．小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标
有1、2、3、4的四块），你认为将其中的哪一些块带去，就能
配一块与原来一样大小的三角形? 应该带（ ）．
A．第1块 B．第2 块 C．第3 块 D．第4块
（第4题图）
5．下图是各种汽车的标志，其中是轴对称图形的有（ ）个．
A．1个 B．2个 C．3个
D．4个
 |
6、如图，下图是汽车行驶速度（千米／时）和时间（分）
的关系图，下列说法其中正确的个数为（ ）
A．1个 B．2个 C．3个 D．4个
（1）汽车行驶时间为40分钟；
（2）AB表示汽车匀速行驶；
（3）在第30分钟时，汽车的速度是90千米／时； （第6题图）
（4）第40分钟时，汽车停下来了．
7．小华利用计算器计算0.×0.时，发现计算器的显示屏上显示如下图的结果，对这个结果表示正确的解释应该是（ ）．
A．1.677025×10—14
B．1.677025×1014
C．（1.677025×10）—14
D．1.677025×10×（—14）
（第7题图）
8．下面给出的事件中，概率为1的事件有（ ）个．
A．0个 B．1个 C．2个 D．3个
（1）打开电视机，正在播放新闻；
（2）太阳每天从东方升起；
（3）“非典型性肺炎”病毒最终一定会被人类征服；
（4）人体吸入大量煤气（一氧化碳）会中毒．
9．下列等式中，计算正确的是（ ）
A．
B．
C．
D．
10．如图，光线a照射到平面镜CD上，然后在平面镜
AB和CD之间来回反射，这时光线的入射角等于反
射角，即∠1＝∠6，∠5＝∠3，∠2＝∠4。若已知
∠1=55°，∠3=75°，那么∠2等与（ ）
A．50° B．55° C．66° D．65° （第10题图）
二、填空题（每小题3分，共30分）
11．多项式3x3y —2xy＋2的次数是 ．
12．要从一张长为40cm、宽为20cm的长方形纸片
（如图）中，剪出长为18cm、宽为12cm的长方形
纸片，则最多能剪出 张． （第12题图）
13．在直角三角形、钝角三角形和锐角三角形这三种三角形中，
有两条高在三角形外部的是 三角形．
14．把一副常用的三角板如图所示拼在一起，那么图中
∠ADE是 度．
（第14题图）
15、用四舍五入法把0.06097精确到千分位后，其有效数字是_________
16. 在10000张有奖明信片中，设有一等奖5个，二等奖10个，三等奖100个，从中随意买1张。
P（获一等奖）=__________，P（获二等奖）=__________，P（获三等奖）=__________。 P（中奖）=__________， P（不中奖）=__________。
17．有一个等腰三角形，边为6 cm， 8 cm那么此等腰三角形的周长是___________。
18. 0.000635用科学记数法保留两个有效数字为 。
19. (3x + 5y)· =9x2－25y2
20.(－b)2·(－b)3·(－b)5=
三、解答题（21、22、23、24每题6分，共24分）
21．计算：
22．求值：
23．.小明某天上午9时骑自行车离开家，15时回家，他有意描绘了离家的距离与时间的变化情况（如图6－32所示）.
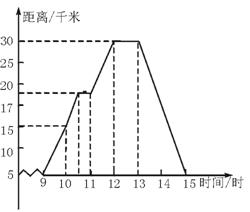
图6－32
（1）图象表示了哪两个变量的关系？哪个是自变量？哪个是因变量？
（2）10时和13时，他分别离家多远？
（3）他到达离家最远的地方是什么时间？离家多远？
（4）11时到12时他行驶了多少千米？
（5）他可能在哪段时间内休息，并吃午餐？
（6）他由离家最远的地方返回时的平均速度是多少？
24．请根据A、B两个题目的要求作图
A题： B题：
如图已知⊿ABC，请你用直尺和圆规作图， 如图已知∠ABC，请你用直尺和圆规作图，作一个三角形，使它和⊿ABC全等。 作一个角，使它等于2∠ABC。
（要求用尺规作图，不必写你是如何作的， （要求用尺规作图，不必写你是如何作的，但是要保留作图时留下的作图痕迹） 但是要保留作图时留下的作图痕迹）
 |
四、解答题（每小题6分，共36分）
25． 如图，有直线AC和DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。以下是他的想法，请你填上根据。
小华是这样想的：
因为CF和BE相交于点O，
根据 得出∠COB＝∠EOF；
而O是CF的中点，那么CO＝FO，又已知 EO＝BO，
根据 得出⊿COB≌⊿FOE， （第19题图）
根据 得出BC＝EF，
根据 得出∠BCO＝∠F，
既然∠BCO＝∠F，根据 出AB∥DF，
既然AB∥DF，根据 得出∠ACE和∠DEC互补。
26．要在已知袋子中装入若干个形状、大小完全相同的小球，使得从袋子中任意摸出一个红球的概率为
，请你给出一种放球的方法。
27．如图，直线a是一个轴对称图形的对称轴，画出这个轴对称图形的另一半，并说明这个轴对称
图形是一个什么图形，它一共有几条对称轴。
 |
（第21题图）
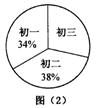
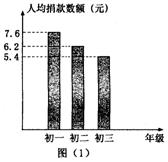28．（6分）去年年底印度洋发生了百年不遇的海啸事件，这个事件给印度洋周边国家带来了巨大的灾难。这一灾难牵动着全世界人民的心，大家纷纷慷慨解囊，给灾区人民献爱心。下面的图（1）是我市某中学“献爱心，抗海啸”自愿捐款活动学生捐款情况制成的条形图，图（2）是该中学学生人数比例分布图，该校共有学生1450人．
（1）初三学生共捐款多少元？
（2）该校学生平均每人捐款多少元？(精确到分)
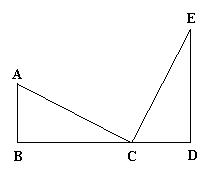29、如图，已知
，
，
，
，那么AC与CE有什么关系？写出你的猜想并说明理由。
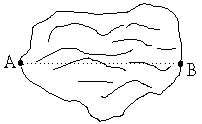
30、如图,在一小水库的两测有A、B两点，A、B间的距离不能直接测得，请用自己学过的知识或方法设计测量方案，求出A、B两点的距离（画出草图;并说明设计方案及理由）。
