七年级下学期数学期中考试3
数 学 试 题
班级__________姓名___________分数_________
一、精心选一选(下列各小题的四个选项中，有且只有一个是符合题意的，把你认为符合题意的答案代号填入答题表中，每小题2分，共26分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 答案 |
1.在同一平面内,两条直线可能的位置关系是( )
A. 平行 B. 相交 C.平行或相交 D. 平行、相交或垂直毛
2.点到直线的距离是( )
A. 点到直线上一点的连线 B. 点到直线的垂线
C. 点到直线的垂线段 D . 点到直线的垂线段的长度
3.判断两角相等,错误的是( )
A.对顶角相等 B两条直线被第三条直线所截,内错角相等
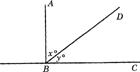
C. 两直线平行,同位角相等 D. ∵∠1=∠2,∠2=∠3,∴∠1=∠3.
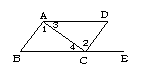
4.如图1，点E在BC的延长线上，则下列条件中，不能判定AB∥CD 的是( )
A. ∠3=∠4 B.∠B=∠DCE C∠1=∠2. D.∠D+∠DAB=180°
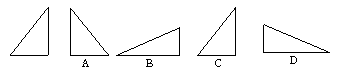
5.下列图中,哪个可以通过左边图形平移得到( )
6、在平面直角坐标系中，点P(－3，2005)在：
A．第一象限 B．第二象限 C．第三象限 D．第四象限
7.已知点P1(-4，3)和P2(-4，-3)，则P1和P2( )
A. 关于x轴对称 B.关于y轴对称
C. 关于原点对称 D.不存在对称关系
8.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比( )
A.向右平移了3个单位 B.向左平移了3个单位
C.向上平移了3个单位 D.向下平移了3个单位
9.点（-7，0）在( )
A.
轴正半轴上 B.
轴负半轴上 C.轴正半轴上 D.轴负半轴上
10.如图，直线EF分别交CD、AB于M、N，且∠EMD=65°，
∠MNB=115°，则下列结论正确的是( )
A.∠A=∠C B.∠E=∠F
C.AE∥FC D.AB∥DC
11、在方程组
、
、
、
、
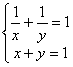、中，是二元一次方程组的有（ ）
A、2个 B、3个 C、4个 D、5个
12、下列各组数中①
②
③
④
是方程
的解的有( )
A.1个
B.2个 C.3个
D.4个
13、如右上图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x、y，那么下面可以求出这两个角的度数的方程组是（ ）
A、
B、
C、
D、
二、细心填一填(每题3分，共21分)
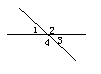
1.如图,已知两直线相交,∠1=30°,则∠2=___,∠3=____,∠4=____.
2.如果两个角是对顶角，且互补，则这两个角都是 角。
3.若直线a⊥b,a∥c,则c___b.
4.命题“同角的补角相等”的题设是______________,结论是_____________________.
5、二元一次方程4x+y=20 的正整数解是______________________。
6. 剧院里5排2号可以用（5，2）表示，则7排4号用 表示.
7.点A的坐标为(3，4),它表示点A在第____象限,它到x轴的距离为_____,到y轴的距
离为_____.
三、学着说点理：(每小题4分，共8分)
1、如图四(1)：∠1＝∠2＝∠3，完成说理过程并注明理由：
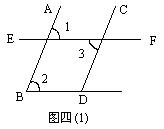(1)因为 ∠1＝∠2
所以 ____∥____ ( )
(2)因为 ∠1＝∠3
所以 ____∥____ ( )
2、如图四(2)：已知AB∥CD，∠1＝∠2.说明BE∥CF.
因为 AB∥CD
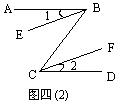所以 ∠ABC＝∠DCB
( )
又 ∠1＝∠2
所以 ∠ABC－∠1＝∠DCB－∠2
即 ∠EBC＝∠FCB
所以 BE∥CF ( )
四、动手画一画：(第1题4分，第2题7分，共11分)
1、如图,将三角形ABC沿AD平移,A点平移
到D, 画出平移后的三角形DEF.
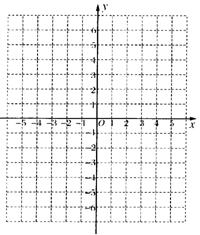2.在图所示的平面直角坐标系中表示下面各点
A（0，3） B（1，-3） C（3，-5）
D（-3，-5） E（3，5） F（5，7）
（1）A点到原点O的距是 。
（2）将点C向轴的负方向平移6个单位，
它与点 重合。
（3）连接CE，则直线CE与轴是什么关系？
（4）点F分别到、轴的距离是多少？
五、认真算一算（每题5分，共20分）
(用代入消元法) 
（用加减消元法）
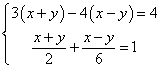
六、请你来解决（第1题6分，第2题8分，共14分）
1、用16元买了60分、80分两种邮票共22枚。60分与80分的邮票各买了多少枚？
2、足球联赛中,某足球队按足协的计分规则与本队奖励方案如下表.
| 胜一场 | 平一场 | 负一场 | |
| 积 分 | 3 | 1 | 0 |
| 奖金(元/人) | 1500 | 700 | 0 |
当比赛进行到第12轮结束时,该队负3场,共积19分.
问：(1)该队胜,平各几场?
(2)若每赛一场,每名参赛队员均得出场费500元,试求该队每名队员在12轮比赛结束后总收入。