七年级数学第二学期期中质量检测
试题
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 |
| 得分 |
一、选择题(每小题3分，共30分)
1.下列方程变形正确的是（ ）.
A.由3+x=5，得x=5+3
B.由7x=-4，得x=-
C.由
y=0，得y=2
D.由3=x-2，得x=-2-3
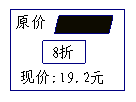
2.右图是“东方”超市中“飘柔”洗发水的价格标签，一服务员不小心将墨水滴在标签上，使得原价看不清楚，请帮忙算一算，该洗发水的原价（ ）.
A.22元 B.23元 C.24元 D.26元
3.关于x、y的二元一次方程组
的解也是二元一次方程2x+3y=6的解，则k的值是（ ）.
A.k=-
B. k=
C. k=
D.
k=-
4. 下列各线段中，能构成三角形的是（
）.
A.6cm、8cm、15cm B.3cm、4cm、5cm
C.2cm、2cm、4cm D.9cm、8cm、1cm
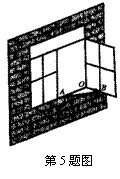
5.如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是 ( ).
A. 三角形的稳定性 B. 两点之间线段最短
C. 两点确定一条直线 D. 垂线段最短
6.如图，天平右盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上可表示为（ ）.
7．已知关于x的不等式2x+m>-5的解集如图所示，则m的值为( ).
A．1
B．0
C．-1 D．-2
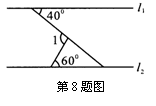8.如图，已知AB∥CD，直线
分别交AB、CD于点E、F，EG平分∠BEF，若∠EFG=40°，则∠EGF的度数是（
）.
A.60° B.70° C.80°
D.90°
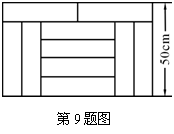
9.如图，宽为50 cm的矩形图案由10个全等的 小长方形拼成，其中一个小长方形的面积为（ ）.
A. 400 cm2 B. 500 cm2
C. 600 cm2 D. 4000 cm2
10.两年期定期储蓄的年利率为2.25%，按国家规定，所
得利息要缴纳20%的利息税.王大爷于2002年6月存入银行一笔钱，两年到期时，共得税后利息540元，则王大爷2002年6月存款额为（ ）元.
A.20000 B.18000 C.15000 D.12800
二、填空题(每小题3分，共30分)
11.已知5x-10y+15=0，用含x的代数式表示y，得 .
12.当x= 时，代数式2（3x+4）的值比5（2y-7）的值大3.
13．若一个一元二次方程的解为
，则这个方程可以是____________
14.已知等腰三角形的两边长分别是6和3，那么它的周长是_____ _．
15.已知关于x的不等式组
的整数解共有5个解，则a的取值范围是 .
16.若三角形三个内角之比为1︰2︰3，则这个三角形是 三角形.
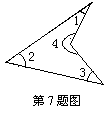
17.如图，∠1+∠2+∠3+∠4= .
18. 在△ABC中，AC=12，AB=8，那么BC的取值范围是 .
19.王老师带领团员到农村搞社会调查.每张票原价为50元，甲车主说：乘我的车可以8折优惠；乙车主说：乘我的车学生9折，老师可以不买票.王老师计算了一下，觉得不论坐哪家的车，付款都一样.则王老师带的学生人数为 人.
20.杉杉打火机厂生产某种型号的打火机，每只的成本为2元，毛利率为25%。工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，则这种打火机每只的成本降低了_________元.(精确到0.01元。毛利率＝)
三、解方程（组）或不等式（组）（每小题6分，共24分）
21.（1）
= 
-1 （2）
（3）解不等式组：
,并将它的解集在数轴上表示出来．
（4）已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立，求A、B的值.
四、解答题（每小题8分，共24分）
22.
23.某校初一年级春游，若租用48座客车若干辆，则正好做满；若租用64座客车，则能少租1辆，且有一辆车没有做满，但超过一半.已知租用48座客车每辆250元，租用64座客车每辆300元，问应租用哪种客车较合算？
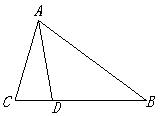24.如图D是△ABC的BC边上一点，∠B=∠BAD，
∠ADC=70°，∠BAC=60°，
求：（1）∠B的度数；（2）∠C的度数.
五、解答题：（本题供选做，若两题都做，按A题记分，12分）
25．A）某水果批发市场香蕉的价格如下表：
| 购买香蕉数 (千克) | 不超过 20千克 | 20千克以上但不超过40千克 | 40千克以上 |
| 每千克价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克(第二次多于第一次)，共付款264元，请问张强第一次、第二次分别购买香蕉多少千克?
B）在华师教材第67页习题9.1中有一道题目：如图1，在△ABC中，∠ABC=80°，∠ACB=50°，BP平分∠ABC，CP平分∠ACB，求∠BPC的度数.
对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）
解：∵BP平分∠ABC（已知），
∴∠PBC=∠ABC=×80°=40°.同理可得∠PCB= .
∵∠BPC+∠PBC+∠PCB=180°（ ）.
∴∠BPC=180°-∠PBC-∠PCB（等式的性质）
=180°-40°- = .
小明在解答过程中，试着将条件“∠ABC=80°，∠ACB=50°”改为“∠ABC=70°，∠ACB=60°”后，发现∠BPC的大小并没有改变，由此他提出了如下三个结论：
（1）如图1中，∠BPC的大小只与∠A的大小有关.
（2）如图2，若P点是∠ACB和外角∠ABE的角平分线的交点. ∠BPC与∠A肯定也有一定的数量关系.
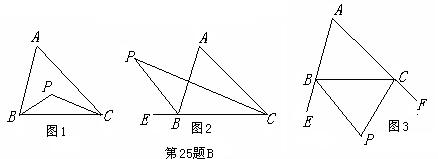（3）如图3，若P点是外角∠CBE和∠BCF的角平分线的交点∠BPC与∠A也有一定的数量关系.
聪明的你，帮助小明将上面的空格填上适当的内容，然后研究他的三个结论是否存在，若存在，请把结论分别用一个式子表示出来，并填在下面的空格中.（1）∠BPC= . （2）∠BPC= .
（3）∠BPC= .
从（2）、（3）两个结论中任选一个，写出你的探索过程.
解：