七年级上学期期中素貭测评数学试卷
第一部分 期中检测（满分100分）
一、填空（每小题2分，共20分）
1．如果水位升高3m时水位变化记作+3m，则水位下降5米时水位变化记作：
2．大于–3且不大于2的所有整数写出来是
3．已知有理数a、b、c在数轴上的位置如图所示，则
0。
4．计算：｜+8｜–｜–7｜+ (–1)2004 –23 =
5．把数用科学记数法记作为
6．直接写出计算结果：–81÷
×
=
7．某商品原价每件x元，第一次降价是打“八折”（按原价的80%出售），第二次降价每件又减少10元,这时的售价是 元。
8．化简：8y –3(3y + 2) =
9．解方程
时，去分母得
=
10．解方程4x + 1 = 3x + 5得，x =
二、选择题（每小题3分，共30分）
11．下列叙述中，正确的是（ ）
A．最大的负数是–1 B．一个数大于它的相反数
C．一个数的绝对值必是正数 D．绝对值最小的数是0
12．已知A地的海拔高度为–53米，B地比A地高30米，则B地的海拔高度为（ ）
A．–83米 B．–23米 C．30米 D．23米
13．点A、B在数轴上，点A表示+1，A、B两点间的距离是3个单位长度，则点B表示的数是（ ）
A．4 B．–2 C．±3 D．4或–2
14．计算–24的结果是（ ）
A．–8 B．8 C．16 D．–16
15．下列叙述正确的是（ ）
A．平方等于本身的数有0、1、–1
B．立方等于本身的数有0、1、–1
C．若｜a｜＞｜b｜，则a3＞b3
D．几个有理数相乘，若有奇数个负因数，则积为负
16．用四舍五入法对数取近似值，保留三个有效数字，结果是（ ）
A．566 B． C．5.66×106 D．5.67×106
17．某班共有x名学生，其中男生占51%，则女生人数为（ ）
A．49%x
B．51%x
C．
D．
18．解方程3x – 4 = 2x + 5，正确的变形是（ ）
A．3x + 2x = 5 – 4 B．3x + 2x = 5 + 4
C．3x – 2x = 5 – 4 D．3x – 2x = 5 + 4
19．下列叙述正确的是( )
A．方程2x = 0的解是x = –2 B．方程
x = 3的解是x = 1
C．方程7x = 11的解是x =
D．方程–
的解是x = –
20．已知关于x的方程ax – 4 = 14x + a的解是x = 2，则a的值是（ ）
A．24 B．–24 C．32 D．–32
三、计算下列各题（每小题4分，共16分）
21．– 40 –28 –（–19）+（–24）–（–32） 22．– 9 + 5×(– 6 ) – 12÷(– 6 )
23． – 24×
24．
四、解方程（每小题4分，共16分）
25．
―1=
； 26．4x + 3 (2x – 3) = 12 – (x + 4)；
27．
；
28．
五、应用题（每小题6分，共18分）
29．某公路检修小组乘汽车沿公路检修路面，约定前进为正，后退为负。某天自A地出发，到收工时所走的线路为（单位：km）：+ 9，–3，+4，–2，–8，+13，–3，+10，+7，+3。
（1）问收工时距A地多远？
（2）若汽车耗油量为0.3kg/km，问从A地出发到收工时共油量多少？
30. （列方程解应用题）甲、乙两人同时加工同样多的同种零件， 甲每小时加工10个零件，乙每小时加工6个零件。当甲完成任务时，乙还剩8个没有完成。问：甲加工了几小时？甲加工完成了多少个零件？
31．（列方程解应用题）小华从甲村走到乙村，若每小时走4千米，那么走到预定时间，离乙村还有0.5千米；如果他每小时走5千米，则比预定时间早到半小时。求：预定时间是多少？甲村到乙村的路程是多少？
第二部分 能力挑战（满分20分）
一、填空与选择（每小题2分，共10分）
1．已知有理数a、b、c在数轴上表示如图所示，则把数
、
、
用“＜”号连接起来是
2．计算：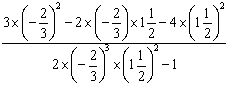
=
3．使式子
的值为正整数的x的值是（
）
A．正数 B．负数 C．零 D．不存在
4．方程
的解是
5．如果a个人b天可以做c个零件（假设每个人的工作效率相同），则b个人用相同的工作效率做a个零件的天数是 天。
二、解答（共10分）
6．解方程｜x –｜3x + 1｜｜= 4（本题3分）
7．甲、乙两人每年的收入相等，甲每年储蓄全年收入的
，乙每月比甲多开支100元，三年后乙负债600元，求每人每年的收入为多少？（本题3分）
8．一次象棋比赛，甲、乙、丙三队共有10名选手参加，每名选手都与其余9名选手各赛一盘，每盘棋胜者得1分，负者得0分，平局各得0.5分。结果甲队选手平均得4.5分，乙队选手平均得3.6分，丙队选手平均得9分，求甲、乙、丙各有几名选手参赛？（本题4分）