初一数学第二学期期中数学试卷
（考试时间：120分钟 满分：150分）
友情提示：
HI，亲爱的同学，你好！今天是展示你才能的时候了，只要你仔细审题、认真答题，把平常的水平发挥出来，你就会有出色的表现，放松一点，相信自己的实力！
| 得分 | 评卷人 |
|
|
|
一、你一定能选对！ （每题3分，共33分。每小题共有四个选项，其中只有一个选项是正确的，将正确选项前的字母填入下表相应的题号下面。）
1、下列现象是数学中的平移的是（ ）
A、秋天的树叶从树上随风飘落 B、电梯由一楼升到顶楼
C、DVD片在光驱中运行 D、“神舟”六号宇宙飞船绕地球运动
2、下列哪个度数可能成为某个多边形的内角和（ ）
A、2400 B、6000 C、19800 D、21800
3、长度为1㎝、2㎝、3㎝、4㎝、5㎝的五条线段，若以其中的三条线段为边构成三角形，可以构成不同的三角形共有（ ）
A、2个 B、3个 C、4个 D、5个
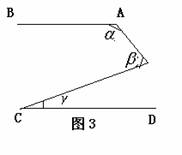
4、如图，若AB∥CD，则
之间的关系为（ ）
A、
B、
C、
D、
5、 下列运算正确的是（ ）
A 
B 
C 
D 
6、生物具有遗传多样性，遗传信息大多储存在DNA分子上。一个DNA分子的直径约为0.cm.，这个数用科学记数法可表示为 （ ）
A．0.2×10—6cm B． 2×10—6cm C． 0.2×10—7cm D． 2×10—7cm
7、多项式有：①
；②
；③
；④
；⑤
；⑥
。以上各式中，形如
的形式的多项式有（ ）
A、2个 B、3个 C、4个 D、5个
8、规定一种运算：a*b=ab+a+b,则a*（-b）+ a*b计算结果为 （ ）
A. 0 B. 2a C. 2b D.2a b
9、方程
的 正整数解为（ ）
A、
B、
C、
D、
10、a = 
, b = 
, c =
，则 a、b 、c 的大小关系是
( )
A. a>c>b B. b>a>c C. b>c>a D. c>b>a
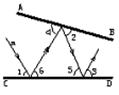11、光线a照射到平面镜CD上，然后在平面镜AB和CD之
间来回反射，光线的反射角等于入射角．若已知∠1=55°，
∠3=75°，则∠2= （ ）
A．50° B．55° C．66° D．65°
| 得分 | 评卷人 |
|
|
|
二、你能填得既快又准吗！（ (每空3分，共30分.)
12、计算
13、在方程5x+3y-3=0中，用含x的代数式表示y,则得 。
14、若
是关于
、
的二元一次方程，则
，
15、若等腰三角形的两边的长分别是3cm、7cm,则它的周长为 cm.
16、如果一个十二边形的每个内角都是相等的，那么这个内角的度数是 。
17、若
为整数）是一个完全平方式，则N＝
。
18、若二元一次方程组
的解是二元一次方程
的一个解，那么a的值是
。
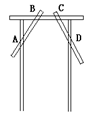
19、木工师傅在做完门框后，为防止变形常常想像右图中所示那样钉上两条斜拉的木板条（即图中的AB、CD两个木条），这样做的数学道理是 。
20、在日常生活中如取款、上网等都需要密码。有一种“因式分解”法产生的密码，方便记忆。原理是：如对于多项式
，因式分解的结果是
，若取
，
时，则各个因式的值是：
，
，
，
于是，就可以把“018162”作为一个六位数的密码。对于多项式
，取
，
时，用上述方法产生的密码是：________________（写出一个即可）。
| 得分 | 评卷人 |
|
|
|
三、算一算，千万别出错！(共38分)
21、(本题满分10分)
(1) 
（2）
其中x=-2。
22、(本题满分10分)分解因式：
（1）
(2)
23、(本题满分8分) 已知
的值。
24、(本题满分10分)解方程组
（1）
(2)
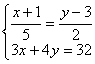
四、简答题：（共49分）
25、 (本题满分9分)画图并填空:
(1)画出图中△ABC的高AD(标注出点D的位置);
(2)画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
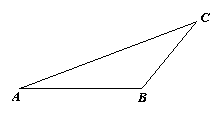(3)根据“图形平移”的性质,得BB1=
cm,AC与A1C1的位置关系是:
.
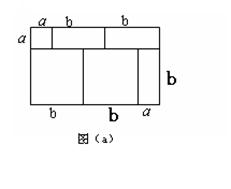
26、(本题满分9分)阅读下列文字：我们知道对于一个图形，通过不同的方法计算图形的面积时，可以得到一个数学等式，例如由图（a）可以得到
．请解答下列问题：
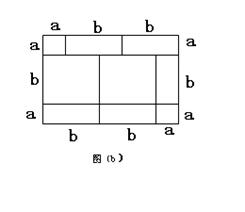
（1）写出图（b）中所表示的数学等式_____________________________；
（2）试画出一个长方形，使得用不同的方法计算它的面积时，能得到
|
| | ||||
| | ||||
|
| |
27、(本题满分16分)请阅读下列材料：
让我们来规定一种运算：
，例如：
再如，
按照这种运算的规定：请解答下列各个问题：
（1）
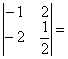（只填最后结果）；
（2）化简
（3）x=
时，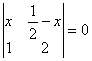
；
（4）求x、y的值，使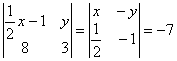
（写出解题过程）。
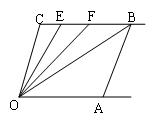28、(本题满分15分)如图，已知射线CB∥OA，∠C=∠OAB=1000，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF。
（1）求∠EOB的度数；
（2）若平行移动AB，那么∠OBC：∠OFC的值是否随之变化？若变化，找出变化规律；若不变，求出这个比值；
（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠0BA？若存在，求出其度数；若不存在，说明理由。