初一数学竞赛试卷七
姓名
一、填空题：（每小题5分，共30分）
1、已知方程组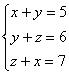
，则2002（x+y+z）= .
2、已知：a2+a=0 则a2001+a2002+12的值是 .
3、若两个自然数的和为100，则这个数积的最大值是 .
4、从1点45分到2点5分，分钟转过的角度是 .
5、若一个角的补角是x0，则这个角的余角是 度.（900＜x0＜1800＝
6、某省有两种手机的收费方式：“小英通”每月话费是10元月租费，加上每分钟0.4元通话费；“神州行”每月话费是25元月租费，加上每分钟0.2元的通话费.若某手机用户估计月通话时间在150分钟左右，则他应选择 方式.
二、选择题（每小题6分，共30分）
1、方程组
的解适合y＞x＞0，则a的取值范围是（
）.
A.-3＜a＜2 B.2＜a＜5 C.1＜a＜4 D.-4＜a＜1
2、已知：x
=2，y=3，则(x2y)
的值是（ ）.
A.48 B.72 C.144 D.不能确定
3、下列形式的数(无论n取什么自然数)中,一定不是某一自然数的平方数的是( ).
A3(n2-n+1) B.5(n2-n+1) C.7(n2+n+1) D.9(n2+n+1)
4、观察下列图形,并阅读图形下面相关文字,由十条直线相交最多交点的个数是( ).
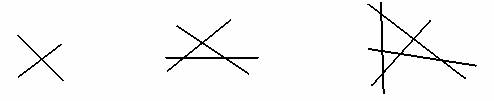
两条直线相交， 三条直线相交， 四条直线相交，
最多1个交点。 最多3个交点。 最多6个交点。
A.40 B.45 C.50 D.55
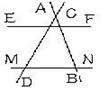
5、如图:若平行直线EF、MN与相交直线AB、CD相交,
则图中共有同旁内角( ).
A.4对 B.8对 C.12对 D.16对
三、解答题
1、已知有理数x、y、z满足x-y=8，xy+z2=-16，求证：x+y+z=0. （满分10分）
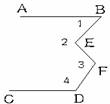
2、如图，AB∥CD，求∠1+∠2+∠3+∠4的度数.（满分10分）
3、先阅读下列一段文字，然后解答问题.（满分20分）
某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食品，并规定：研制成的混合食品中至少需要44000单位的维生素A和48000单位的维生素B.三种食物中维生素A、B的含量如下表所示.
表Ⅰ
|
| 甲 种 | 乙 种 | 丙 种 |
| 维生素A（单位/千克） | 400 | 600 | 400 |
| 维生素B（单位/千克） | 800 | 200 | 400 |
表Ⅱ
|
| 每千克生产成本（元） |
| 甲 种 | 9 |
| 乙 种 | 12 |
| 丙 种 | 8 |
设研制生产甲、乙、丙三种食物的质量分别为x千克、y千克、z千克.
①试根据题意列出等式和不等式，并证明：y≥20，2x-y≥40.
②设甲、乙、丙三种食物的生产成本如表Ⅱ所示，试用含x、y的代数式表示研制的混合食品的总成本P；若限定混合食品中甲种食物的质量为40千克，试求出此时总成本P的取值范围，并确定当P取最小值时，所取乙、丙两种食物的质量.