9.1.1 不等式及其解集
1.用 连接的式子叫做不等式；
2.在下列各题中的空白处填上适当的不等号：
⑴ －3 －2 ⑵ 
⑶
－2；
3.用适当的符号表示下列关系：⑴ a－b是负数 ，⑵ a比1大 ， ⑶ x是非负数 ，⑷ m不大于－5 ，
⑸ x的4倍大于3 ；4.正方形边长是xcm，它的周长不超过160cm，则用不等式来表示为 ；
5.直接想出不等式的解集：
⑴ x＋3＞6的解集 ，⑵ 2x＜12的解集 ，⑶ x－5＞0的解集 ，⑷ 0.5x＞5的解集 ；
6.含有 个未知数，未知数的次数是 的不等式叫做一元一次不等式；
7.某班同学外出春游，要拍照合影留念，若一张彩色底片需要0.57元，冲印一张需0.35元，每人预定得到
一张，出钱不超过0.45元，设合影的同学至少有x人，则可列不等式 ；
8.x的3倍减去2的差不大于0，列出不等式是 （ ） A、3x－2≤0 B、3x－2≥0 C、3x－2＜0 D、3x－2＞0
9.当x = 3时，下列不等式成立的是 （ ） A、x＋3＞5 B、x＋3＞6 C、x＋3＞7 D、x＋3＞8
10.下列不等式一定成立的是
（ ）A、2x＜6 B、－x＜0 C、
＞0 D、
＞0
11.下列解集中，不包括－4的是 （ ）A、x≤－3 B、x≥－4 C、x≤－5 D、x≥－6
12.下列说法中，正确的有 （ ）
①4是不等式x＋3＞6的解，②x＋3＜6的解是x＜2③3是不等式x＋3≤6的解，④x＞4是不等式x＋3≥6的解的一部分
A、1个 B、2个 C、3个 D、4个
13.图中表示的是不等式的解集，其中错误的是（ ）
A、x≥－2
B、x＜1
C、x≠0
D、x＜0
14.－3x≤6的解集是 （ ）
A、
B、
C、
D、
15.恩格尔系数n是指家庭日常饮食开支占家庭收入的比例，它反映了居民家庭的实际生活水平，各种类型
家庭的n值如下所示：
| 家庭类型 | 贫困 | 温饱 | 小康 | 发达 国家 | 最富裕国家 |
| n | 75% 以上 | 50% ～75% | 40% ～49% | 20% ～39% | 不到20% |
如用含n的不等式表示，则贫困家庭为 ；小康家庭为 ；最富裕国家为 ；
当某一家庭n = 0.6时，表明该家庭的实际生活水平是 。
16.比较下面两个算式结果的大小（在横线上填“＞”“＜”“＝”）
通过观察归纳，写出能反映这种规律的一般情况：
。
17.工人张力4月份计划生产零件176个，前10天平均每天生产4个，后来改进技术，提前3天并且超额完成任务，若张力10天之后平均每天至少生产零件x个，请你试着写出x所满足的关系式。
18.写出下列不等式的解集，并把解集在数轴上表示出来：⑴ x＋5＞7 ⑵ 2x≤10 ⑶ x－2＞1 ⑷ -3x＜12
19.一种饮料重约300g，罐上注有“蛋白质含量≥0.5%”，其中蛋白质的含量为多少克？
20.2004年1月20日，湖北省武穴市石佛寺镇发生高致病性禽流感，疫情发生后，党中央和国家领导人高度重视，温家宝总理亲赴疫情一线指挥扑疫工作，为防止疫情的进一步扩散，对疫点3公里以内的53711只.禽类全部捕杀，对3公里以外5公里以内的14万只禽类进行紧急预防接种，对疫点及周边3公里以内住户的畜禽生产场地进行消毒，为免除农户的后顾之忧，国家规定，对按规定捕杀的家禽给予合理的补偿，
对家禽强制免疫实行免费，给一只家禽预防接种需费用1.5元，对周边环境消毒共用资金不多于90万元，武穴市用于此次疫情的总资金为200万元，设对按规定捕杀的禽类每只赔给农户x元，请你列出表示这个问题中的不等关系的不等式。
9.1.2 不等式的性质
1.用a＞b，用“＜”或“＞”填空：
⑴ a＋2 b＋2 ⑵ 3a 3b ⑶ －2a －2b⑷ a－b 0 ⑸ －a－4 －b－4 ⑹ a－2 b－2；
2. 用“＜”或“＞”填空：
⑴若a－b＜c－b，则a c ⑵若3a＞3b，则a b⑶若－a＜－b，则a b ⑷若2a＋1＜2b＋1，则a b
3.已知
＞b，若＜0则
b，若＞0则 b；
4. 用“＜”或“＞”填空：
⑴ 若a－b＞a则b 0 ⑵ 若
＞
则 b ⑶ 若a＜－b 则
a －b
⑷ 若a＜b则a－b 0 ⑸ 若a＜0，b 0时ab≥0
5.若
＜
，则一定满足
（ ） A、＞0 B、＜0 C、≥0 D、≤0
6.若x＞－y，则下列不等式中成立的有 （ ） A、x＋y＜0 B、x－y＞0 C、x＞
y D、3x+3y＞0
7.若0＜x＜1，则下列不等式成立的是 （ ） A、
＞
＞
B、＞＞
C、＞＞ D、＞＞
8.若方程组
的解为x，y，且x+y＞0，则k的范围是 （ ）A、k＞4 B、k＞－4 C、k＜4 D、k＜－4
9.用不等式表示下列各式，并利用不等式性质解不等式。
⑴a的
是非负数
⑵m的2倍与1的和小于7
⑶a与4的和的20%不大于－5
⑷x的
与x的3倍的和是非负数。
10.下列4种说法：① x = 
是不等式4x－5＞0的解
② x = 
是不等式4x－5＞0的一个解
③ x＞是不等式4x－5＞0的解集
④ x＞2中任何一个数都可以使不等式4x－5＞0成
立，所以x＞2也是它的解集，其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个
11.某种商品进价为150元，出售时标价为225元，由于销售情况不好，商品准备降价出售，但要保证利润不低于10%，那么商店最多降多少元出售此商品。
12.有一个两位数，个位上的数是m，十位上的数是n如果把这个两位数的个位与十位数字对调，得到的两位数大于原来的两位数，那么m与n哪个大？
13.一个长方形足球场的长为x米，宽为70米，如果它的周长大于350米，面积小于7560米2，求x的取值范围，并判断这个球场是否可以用作国际足球比赛。 （注：用于国际比赛的足球场的长在100米到110米之间，宽在64米到75米之间）
14.有1千克含40克食盐的咸水，再加入食盐，使它成为浓度不小于20%的食盐水，应加入多少克食盐？
15.哥哥存款600元，弟弟存款2000元，由本月开始，哥哥每月存款500元，弟弟每月存款200元，试问到了第几月哥哥的存款能超过弟弟的存款？
16.某次数学测试工16题，满分100分，评分办法是：答对一道给6分，答错一道扣2分，不答不给分，某学生有一道题未答，那么他至少要答对多少道题才及格？（及格60分）
.2 实际问题与一元一次方程
1.3x＞－6的解集是 ，
＜－8的解集是 ；2.当m 时，不等式mx＜5m的解集是x＞5；
3.若2－a＞－2a成立，则a ；4.不等式
≥
的解集为 ；
5.若使代数式
的值不大于
的值，则x的取值范围为
；
6.使不等式x－2≤3x+5成立的负整数为 ；7.不等式4x－6≥7x－12的非负整数解为 ；
8.代数式
的值大于1，则y的取值范围是
；
9.某人10点10分离家赶11点整的火车，已知他家离车站10公里，他离家后先以3公里/时的速度走了5分
钟，然后乘公共汽车去车站，公共汽车每小时至少走 公里才能不误当次火车；
10.某试卷共有20道题，每道题选对了得10分，选错了或不选的扣5分，至少要选对 道题，其得分才能不少于80分；
11.3x－7≥4（x－1）的解集是 （ ）A、x≥3 B、x≤3 C、x≥－3 D、x≤－3
12.14x－7（3x－8）＜4（25＋x）的负整数解是 （ ）A、－3，－2，－1 B、－1，－2C、－4，－3，－2，－1 D、－3，－2，－1，0
13.若不等式ax＞b的解集是x＞
，则a的范围是（ ）A、a≥0 B、a≤0 C、a＞0 D、a＜0
14.不等式
≤3的解集是
（ ） A、x≤4 B、x＜4 C、x≤7 D、x≤5
15.不等式
＜
的解集是
（ ） A、全体有理数 B、全体正数 C、全体负数 D、无解
16.2x＋1是不小于－3的负数，表示为 （ ） A、－3≤2x＋1≤0 B、－3＜2x＋1＜0 C、－3≤2x＋1＜0 D、－3＜2x＋1≤0
17.与不等式
＜
有相同解集的是 （ ）
A、3x－3＜（4x+1）-1 B、3（x－3）＜2（4x+1）-1 C、2（x－3）＜3（2x＋1）－6 D、3x－9＜4x－4
18.解不等式
＞
的过程中，出现错误的一步
的是 ① 去分母：5（x＋2）＞3（2x－1）② 去括号：5x＋10＞6x－3③ 移项：5x－6x＞－10－3 ④系数化为1：x＞13
A、① B、② C、③ D、④
19.解下列不等式，并把解集在数轴上表示出来：
⑴ 
＜
⑵ 
≤1
⑶
≤ 
⑷
＞-2
0.x为何值时，代数式
不大于的值。 21.求不等式
≤
的非负数解。
22.若
＜
的最小整数解是方程 
的解，求代数式
的值。
23.小明准备用21元钱买笔和笔记本，已知每支笔3元，每个笔记本2.2元，他买了两个笔记本，请你帮他算一算，他还可以买几支笔？
24.m是什么正整数时，方程
的解是非
25.红星公司要招聘A、B两个工种的工人150人，A、B工种的工人的月工资分别为600和1000元，现要求B工种的人数不少于A工种人数的2倍，那么招聘A工种工人多少时，可使每月所付的工资最少？此时每月工资为多少元？
9.3 一元一次不等式组
1.不等式组
的解集为 ，
的解集为 ，
的解集为 ，
的解集为 ；
2.不等式-2≤x-5＜6的解集是 ；
3.不等式组
的解集为
，不等式组
的解集为
；
4.不等式-1＜
≤2的整数解的和为
；
5.不等式组
的解集为x＞2，则的范围是 ；
6.不等式组
的解集为
；
7.长度分别为3cm，7cm，xcm的三根木棒围成一个三角形，则x的取值范围是 ；
8.不等式组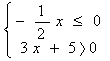
的解集为 （ ） A、
＜x≤
B、x＞ C、x≥0 D、x≥－2
9.不等式组
的非负整数解的个数为（ ） A、2个 B、1个 C、0个 D、无数多个
10. 一种灭虫药粉30kg，含药率是15%，现在要用含药率较高的同种灭虫药粉50kg和它混合，使混合后的含药率大于20%且小于35%，则所用药粉的含药率x的范围是 （ ）
A、15%＜x＜23% B、15%＜x＜35% C、23%＜x＜47% D、23%＜x＜50%
11.解下列不等式组，并把解集在数轴上表示出来：
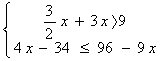⑴
⑵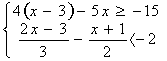
⑶
⑷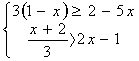
12.关于x的不等式组
的着整数共有5个，则的取值范围是
。
13.若不等式组
的解集为－1＜x＜2，则=
，b = 。
14.不等式组
的解集为x＜3＋2，则的取值范围是
。
15.若不等式组
无解，则m的取值范围是 。
16.k取何值时，方程组
中的x大于1，y小于1。
17.一群女生住若干家间宿舍，每间住4人，剩下19人无房住；每间住6人，有一间宿舍住不满。
⑴ 如果有x间宿舍，那么可以列出关于x的不等式组： ；
⑵ 可能有多少间宿舍、多少名学生？你得到几个解？它符合题意吗？
9.4 利用不等关系分析比赛
1.某工厂试制新产品，工本费共700元每只售价2元，试问在保证有多于1000元以上利润的情况下，售出的产品数量的范围是多少？
2.某市自来水公司按如下标准收取水费：若每户每月用水不超过5
，则每立方米收费1.5元，若每户每月用水超过5，则超出部分每立方米收费2元，小强家某月的水费不少于15元，那么他家这个月的用水量至少是多少？
3.某种植物适宜生长在温度18～20℃的山地，已知山区海拔每升高100米气温下降0.55℃，现测出山脚下的平均气温为22℃，问该植物种在山的哪一部分为宜？
4.每期《数理天地》（初中版）发下来后，秦同学都认真阅读，他如果每天读5页，9天读不完，第10天不足5页；如果每天读23页，那么两天读不完，第3天剩不足23页，试问《数理天地》（初中版）杂志每期有多少页？（页数为偶数）
5.有人问一位老师他所教的班上有多少学生，老师说：“一半的学生在学数学，四分之一的学生在学音乐，七分之一的学生在读外语，不足六位同学在操场上踢足球。”试问这个班共有多少名学生？
6.我市某化工厂现有甲种原料290千克，乙种原料212千克，计划利用这两种原料生产A、B两种产品共80件，生产一件A产品需要甲种原料5千克，乙种原料1.5千克；生产一件B种产品需要甲种原料2.5千克，乙种原料3.5千克，该化工厂现有的原料能否保证生
产顺利进行？若能的话，有几种方案？请你设计出来。
7.某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备送给他们，如果每人送3本，则还余8本；如果前面每人送5本，则最后一人得到的课外读物不足3本；设该校买了m本课外读物，有x名学生获奖，请解答下列问题： ⑴ 用含x的代数式表示m；
⑵ 求该校的获奖人数及所买课外读物的本数。
8.商场出售的A型冰箱每台售价2190元，每月耗电量为1千瓦·时，B型冰箱每台售价比A型冰箱高出10%，但每日耗电量却为0.55千瓦·时，商场将A型冰箱打折销售，如果只考虑价格与耗电量，那么至少打几折消费者购买才合算？（使用期为10年，每年365天，
每千瓦·时电费按0.4元计算）