初一《迎春杯》数学科普活动日题目
问题一．2003年10月15日9时，航天英雄杨利伟乘“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行．飞船绕地球飞行了十四圈以后，于16日5时59分返回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约600000千米，计算飞船巡天飞行的平均速度是每秒 千米（结果精确到个位）．
问题二．如果两个角的和等于180°，称这两个角互为补角．
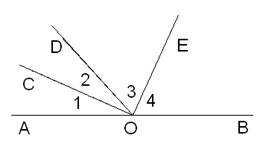
如图，0为直线AB上的一点，若∠1=∠2，∠3=∠4，则图中互为补角的角共有 对．
问题三．观察、分析下列数表中各行、各列数字排列的规律，按照这个规律数表中右下角括号中的数是 ．
| 2 | 4 | 6 | 8 | 10 | … | 2004 |
| 4 | 6 | 8 | 10 | 12 | … | … |
| 6 | 8 | 10 | 12 | 14 | … | … |
| 8 | 10 | 12 | 14 | 16 | … | … |
| 10 | 12 | 14 | 16 | 18 | … | … |
| … | … | … | … | … | … | … |
| 2004 | … … … … … | （ ） | ||||
问题四．当
分别等于
，
，
，
，
，
，
，
，
，
时，计算代数式
的值，将所得的结果相加，其和等于 ．
问题五．用符号“⊕”定义一种运算：对于有理数
，
，
有⊕b=
．
如果2004⊕=2,那么的值等于 .
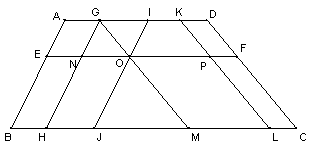
问题六．如图，在梯形ABCD中，EF与AD、BC平行，GH、IJ分别与AB平行，GM、KL分别与DC平行，图中共有 个梯形．
问题七．甲、乙、丙三人一起进行百米赛跑(假定三人均为匀速直线运动)．如果当甲到达终点时，乙距终点还有5米，丙距终点还有10米，那么当乙到达终点时，丙距终点还有 米．
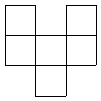
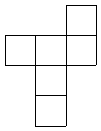
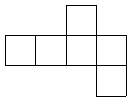
问题八． 在下面六个图形中，每个图形全由6个边长为1的小正方形组成，如果把每个图形沿外轮廓线用剪刀剪下来，能够按照小正方形的边线折叠成棱长为1的正方体的图形共有 个．
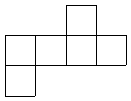
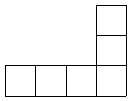
问题九．某学校2004年计划用不超过4500元的经费，资助A、B两类家庭经济困难的学生(每类有若干人).其中A类学生每人资助500元，B类学生每人资助300元．根据学校实际情况，资助A类学生至少4人，资助B类学生至少3人，那么该学校这项资助活动共有不同方案 种．
问题十．已知两个自然数，它们的和是1576，如果分别把这两个数的数字的顺序倒过来以后，它们的和是4375，那么这两个自然数分别是 ．