初一数学竞赛训练题一
一、选择题
1、若abc为非零数，且a+b+c=0,则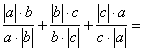
（ ）
A、1 B、－1 C、3 D、－3
2、若方程
的解是正数，则a的取值范围是（ ）
A、
B、
C、
D、
3、已知－1
下列不等式①
②
，③
④
中成立扔（ ）个
A、0 B、1 C、2 D、3
4、若船逆流航行时，船中一物掉入水中， 随水顺流漂行，经t小时后船主发现，此时，船主立即掉头追捞，则需（ ）小时追到。
A、2t B、t C、t+1 D、不能确定
5、蓄不池装有甲、丙两条进水管，和乙、丁两条排水管，要注滿一池水，单开甲管需要3小时，单开丙管需要5小时，要排完一池水，单开乙管需要4小时，单开丁管需要6小时，现知池内
池水，如果按甲、乙、丙、丁、甲、乙、丙、丁、……，顺序轮流各开一小时，则（ ）时间后，水开始溢出水池。
A、
B、
C、
D、以上答案都不对
6．龟兔赛跑，全程5.2千米，兔子每小时跑20千米，乌龟每小时3千米，乌龟不停地跑，但兔子却边走边玩，它先跑1分钟后玩20分钟，又跑2分钟然后玩20分钟，再跑3分钟然后玩20分钟，……，问誰先到达到终点，先几分钟到达终点？（ ）
A、乌龟先11.6分钟 B、兔子先11.6分钟 C、兔子先12.6分钟 D、乌龟先12.6分钟
7、一面钟的时针与分针均指在4与6之间，且钟面上的“5”字恰好在时针与分钟的正中央，问这时是什么时刻？ （ ）
A、4点
分钟 B、5点
分钟 C、4点分钟或5点分钟 D、以上答案都不对
8、某人在x年时，他的年龄正好是出生年的数字之和，而x正是方程2＊x＝（16＊7）的解，其中“＊”是一种运算，定义为a＊b=ab,则此人出生于（ ）年。
A、1970 B、1971 C、1972 D、1973
二、填空题
9、当正整数m=_________时，代数式
的值也是正整数。
10、已知方程组
的解应为
一个学生解题时把c抄错了，因此得到解为
则a2+b2+c2=_________________.
11、某商店原来将一批苹果按100%的利润定价出售，由于定价过高，无人购买，不得不按38%的利润重新定价，这样售出了其中的40%，此时，因害怕剩余水果腐烂变质，不得不再次降价，售出了剩余的全部水果，结果获得的总利润是原定利润的30.2%，则第二次降价后的价格是原定价的百分之______________.
12、已知a<0,-1<b<0,则a , ab , ab2之间的大小关系是______________.
13、已知
14、在一次数学竞赛中，共出了10道题，评分办法是答对一题得4分，答错一题得－1分，不答得0分，若这次竞赛至多有n种不同得分，则n为______________.
15、设
，则正整数x的各位数字之和是______________.
16、设标有A、B、C、D、E、F记号的7盏灯顺次排成一行，每盏灯安装着一个开关，现在A，C，D，G 4盏灯亮着，其余3盏灯是灭的，小方从灯A开始顺次拉动开关，即从A到G，再从A开始顺次拉动开关，他这样拉动了1990次，则亮着的灯是____________。
三、解答题
| 1 | 2 | 5 | 10 | 17 | …… |
| 4 | 3 | 6 | 11 | 18 | …… |
| 9 | 8 | 7 | 12 | 19 | …… |
| 16 | 15 | 14 | 13 | 20 | …… |
| 25 | 24 | 23 | 22 | 21 | …… |
| …… |
17、自然数如下表的规律排列，
(1) 求上起第10行，左起第13列的数？
(2) 数127应排在上起第几列，左起第几行？
(3) 数2000应排在上起第几行，左起第几列？
18．某三位数，如果它本身增加3，则新的三位数的各位数字之和就减少到原来三位数的各位数字之和的
，求这样的所有三位数。
19、某书店对顾客实行一项优惠措施：每次买书200元至499.99元者优惠5%，每次买书500元以上者（包含500元）优惠10%，某顾客到书店买了三次书，如果第一次与第二次合并一起买，比分开买便宜13.5元，如果三次合并一起买比三次分开买便宜39.4元，已经知道第一次的书价是第三次书价的
，问这位顾客第二次买了多少钱的书？
20．将1、2、3、4、5、6、7、8、9这9个数字分别填入下面图（1）中的各个小圈内，要求是：其中任意两个相邻的差不小于3且不大于5。能不能把1到11的11个数、1到12的12个数、1到14的14个数分别填入图中各小圈中，也满足上述条件？如果能，就在图中填好，如果不能，请说明理由。
