初一数学试卷3
(时间: 90分钟 满分: 100分)
一、填空:
(![]() )
)
1. 已知方程![]() , 用含
, 用含![]() 的代数式表示
的代数式表示![]() 为
.
为
.
2. 二元一次方程![]() 的正整数数解是
.
的正整数数解是
.
3. 在⊿ABC中,∠A━∠B![]()
![]() , ∠A
, ∠A![]() ∠B
∠B![]()
![]() , 则∠B
, 则∠B![]() , ∠C
, ∠C![]() .
.
4. 若![]() 是方程组
是方程组![]() 的解, 则
的解, 则![]() .
.
5. 已知方程![]() 是关于
是关于![]() 、
、![]() 的二元一次方程, 则
的二元一次方程, 则![]() .
.
☆6. 若![]()
![]() , 则
, 则![]() .
.
7. 若![]() 是方程
是方程![]() 的解, 则
的解, 则![]() .
.
8. 已知一个三角形的三条边长为![]() 、
、![]() 、
、![]() , 则
, 则![]() 的取值范围是
.
的取值范围是
.
☆9. 已知两个多边形的边数之差为![]() , 它们的内角和为
, 它们的内角和为![]() , 则这两个多边形的边数分别是
.
, 则这两个多边形的边数分别是
.
二、选择: (![]() )
)
10. 在 ①![]() , ②
, ②![]() , ③
, ③![]() , ④
, ④![]() , ⑤
, ⑤![]() ,
,
⑥![]() 中, 二元一次方程有-------------------------------------------【
】
中, 二元一次方程有-------------------------------------------【
】
A、 1个 B、2个 C、3个 D、4个
☆11. 已知方程组![]() , 则
, 则![]() 、
、![]() 的关系为---------------------------------------【
】
的关系为---------------------------------------【
】
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12. 小张用15元买8角和6角的邮票, 钱刚好用完, 则小张的的买法有---------【 】
A、5种 B、6种 C、7种 D、8种
13. 已知![]() 是二元一次方程, 则
是二元一次方程, 则![]() 的取值是--------------------------【
】
的取值是--------------------------【
】
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
14. 已知![]() 和
和![]() 都满足方程
都满足方程![]() , 则
, 则![]() 、
、![]() 的值分别为----【
】
的值分别为----【
】
A、![]() 、
、![]() B、
B、![]() 、
、![]() C、
C、![]() 、
、![]() D、
D、![]() 、
、![]()
15.
三个二元一次方程![]() ,
, ![]() ,
, ![]() 有公共解
有公共解
的条件是-----------------------------------------------------------------------------------【 】
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
☆16. 若方程组![]() 的解也是二元一次方程
的解也是二元一次方程![]() 的一个解,
的一个解,
则![]() 的值为-------------------------------------------------------------------------------【
】
的值为-------------------------------------------------------------------------------【
】
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
17. 在等式![]() 中, 当
中, 当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() . 则
. 则![]() 的值【 】
的值【 】
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
18、甲、乙两个药品仓库共存药品![]() 吨,现从甲仓库调出库存药品的
吨,现从甲仓库调出库存药品的![]() %,从乙仓库调出库存药品的
%,从乙仓库调出库存药品的![]() %,支援灾区, 结果乙仓库所余药品比甲仓库所余药品多
%,支援灾区, 结果乙仓库所余药品比甲仓库所余药品多![]() 吨, 那么甲、乙两仓库原来所存药品分别为----------------------------------------------【
】
吨, 那么甲、乙两仓库原来所存药品分别为----------------------------------------------【
】
A、![]() 吨、
吨、![]() 吨 B、
吨 B、![]() 吨、
吨、![]() 吨 C、
吨 C、![]() 吨、
吨、![]() 吨 D、
吨 D、![]() 吨、
吨、![]() 吨
吨
19. 若![]() , 且
, 且![]() , 则
, 则![]() 等于----------------------------【
】
等于----------------------------【
】
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、解方程组(![]() ):
):
20. 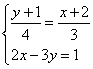 21.
21. 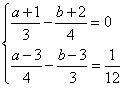
22. ![]() 23.
23.
![]()
四、解答题(![]() ):
):
24. 设满足方程组![]() 的解
的解![]() 与
与![]() 之和为
之和为![]() . 求
. 求![]() 的值.
的值.
25. 在解关于![]() 、
、![]() 的方程组
的方程组![]() 时, 甲正确地解得
时, 甲正确地解得![]() ; 乙因把
; 乙因把![]() 抄错了,
抄错了,![]() 解得
解得![]() , 求
, 求![]() 、
、![]() 、
、![]() .
.
26、 对于有理数![]() 、
、![]() 定义一种运算“△” :
定义一种运算“△” :![]() △
△![]() , 其中
, 其中![]() 、
、![]() 为常
为常
数, 等式右边是通常的加法与乘法运算, 已知![]() △
△![]() ,
, ![]() △
△![]() ,
,
试求 ![]() △
△![]() 的值.
的值.
五、应用题(![]() ):
):
27. 运往某地两批货物, 第一批360 ![]() , 用6节火车皮再加上15辆汽车正好运完; 第二
, 用6节火车皮再加上15辆汽车正好运完; 第二
批440 ![]() , 用8节火车皮再加上10辆汽车正好运完. 求每节火车皮和每辆汽车平均各装多少吨?
, 用8节火车皮再加上10辆汽车正好运完. 求每节火车皮和每辆汽车平均各装多少吨?
28. 某商场计划拨款9万元从厂家购进50台电视机. 已知该厂家生产三种不同型号的电视机, 出厂价分别为: 甲种每台1500元, 乙种每台2100元, 丙种每台2500元 .
⑴若商场同时购进其中两种不同型号电视机50台, 用去90000元, 请你研究一下, 商场有几种进货方案.
⑵若商场销售一台甲种电视机可获利150元, 销售一台乙种电视机可获利200元,
销售一台丙种电视机可获利250元 . 在同时购进两种不同型号电视机的方案种, 为使销售获利最多, 你选择哪种进货方案?
Made by Zhao hui
Checked by Jiangzhihua
附加题:
|

2. 国泰玩具厂工人的工作时间:每月25天,每天8小时。待遇:按件计酬,多劳多得,每月另加福利工资100元,按月结算。该厂生产A、B两种产品,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬1.40元。下表记录了工人小李的工作情况:
| 生产A种产品件数(件) | 生产B种产品件数(件) | 总时间(分) |
| 1 | 1 | 35 |
| 3 | 2 | 85 |
根据上表提供的信息,请回答下列问题:
(1)小李每生产一件A种产品、每生产一件B种产品,分别需要多少分钟?
(2)如果生产各种产品的数目没有限制,那么小李每月的工资数目在什么范围之内?