初一数学下能力测试题（20）
班级_______姓名________
一、填空题
1、在△ABC中，∠A=3∠B=
∠C，则∠A= ，∠B= ，∠C= ；若∠A+∠B=∠C，则△ABC是 三角形
2、已知：△ABC≌△DEF，若△ABC的周长为32cm，AB=8cm，BC=14cm，则DE= cm，EF= cm，DF= cm
3、在△ABC中，若AB=7，BC=5，则 <AC< ；若AB=BC=10，则 <AC<
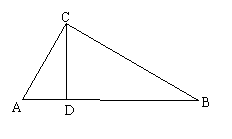
4、如图，在直角三角形ABC中，∠ACB=900，
CD⊥AB于点D，则图中有 个直角三角形，
它们是 ；
∠A是 和 公共角；
互余的角有 几对，它们是
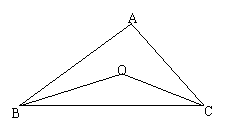
5、如图，已知在△ABC中，∠ABC，∠ACB的平分线相交于点O，
（1）若∠ABC=500，∠ACB=650，则∠BOC= ；
（2）若∠ABC+∠ACB=1300，则∠BOC= ；
（3）若∠A=900，则∠BOC= ；
（4）若∠BOC=1000，则∠A=
6、两根木棒的长分别为3cm和5cm，要选择第三根木棒，将它们钉成一个三角形，当第三根木棒长为偶数厘米时，它的长为 cm
7、若直角三角形的两锐角的差为200，则两锐角的度数分别是
8、如图8，若∠B=300，∠AOB=1100，CE∥AB，则∠ODE= 0，∠OCD= 0
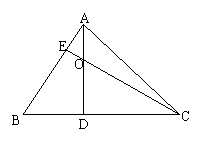
9、如图9，已知△ABC中，AD⊥BC，CE⊥AB，若∠B=500，则∠AOC=
0；
若∠AOC=2∠B时，则∠B= 0
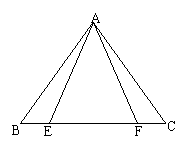
10、如图10，若△ABF≌△ACE，则对应相等的边为 ；对应相等的角为
二、选择题
1、三角形的三边的长可以为下列哪一组（ ）
A、1，2，3 B、8，3，5 C、2，5，10 D、10，10，2
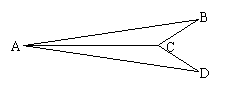2、如图，要使得△ABC≌△ADC，还需要（
）
A、AB=AD，∠B=∠D B、AB=AD，∠ACB=∠ACD
C、BC=DC，∠BCA=∠DCA D、AB=AD，∠BCA=∠DCA
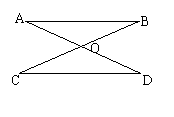3、如图，O为AC的中点，只加上（ ）
则△AOB与△COD不全等，
A、∠A=∠C B、∠B=∠D
C、AB=CD D、OB=OD
4、以长为10cm，7cm，5cm，3cm的四条线段中的三条为边，可画三角形的个数为（ ）
A、1 B、2 C、3 D、4
5、三角形的高是指（ ）
A、从三角形的一个顶点向另一边画的垂线
B、从三角形的一个顶点向另一边画的垂线段的长度
C、从三角形的一个顶点向它的对边画垂线，顶点与垂足间的线段
D、从顶点向对边所画的垂线
6、如图中，∠A+∠B+∠C+∠D+∠E=（ ）
A、1800 B、2400
C、3600 D、4800
三、证明题
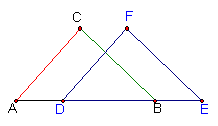
1、如图，已知：AC=AD,BC=BD， 2、如图，已知：AC=DF,BC=EF,AD=BE你能判
试问△ACB与△ADB全等吗？ 定△ABC≌△DEF吗？说说你的理由。
说说你的理由。
3、如图△ABC中，AB=AC，AD是中线， 4、如图中，已知AB∥CD，AB=CD
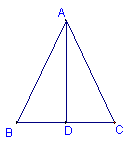请你说出两个正确的结论，并加以证明
求证：∠B=∠D
 |
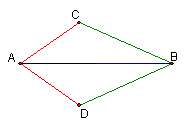
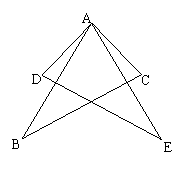5、已知，AC=AD，∠CAB=∠DAB，求证：△ABC≌△ABD
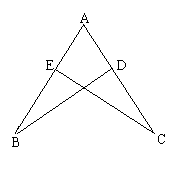6、如图，已知AB=AC，AD=AE，求证：∠B=∠C
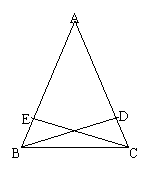7、已知△ABC中，AB=AC，BD⊥AC，CE⊥AB，求证：BD=CE
8、如图，已知，AB=AE，AD=AC，且
∠DAB=∠CAE，求证：∠B=∠E
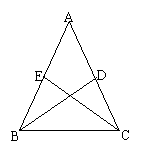9、如图，已知AB=AC，且D、E分别是AB和AC的中点，求证：BD=CE
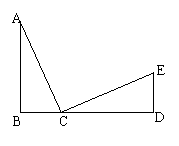
10、如图，已知AB⊥BD，ED⊥BD，
AC⊥CE，且AB=CD，求证：AC=CE
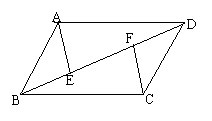11、如图，已知AB=CD，AD=BC，且
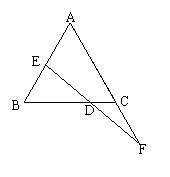AE∥CF，求证：AE=CF
12、如图，已知AB=AC，AD平分∠BAC，且点E在AD上，求证：BE=CE
 |
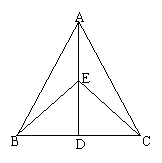
13、如图，已知AB=AC，AD=AE，CE与BE相交于点O，求证：
（1）∠B=∠C （2）OB=OC
14、已知等边三角形ABC中，延长AC到F，使得ED=DF，求证：BE=CF
15、已知等腰直角三角形ABC中，
∠A=900，AB=AC，BE平分∠ABC，
求证：BC=AB+AE
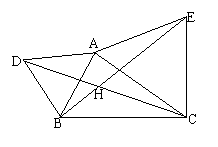
16、已知△ABC中，向外作两个等边三角形AEC，和ABE，求证：（1）CD=BE
（2）求∠BHC