初一年级数学夏令营测试题
一 选择题
1．设a、b、c的平均数为Ｍ，a、b的平均数为Ｎ，Ｎ、c的平均数为P，若a＞b＞c，则Ｍ与Ｐ的大小关系是（ ）.
（Ａ）Ｍ＝Ｐ （Ｂ）Ｍ＞Ｐ （Ｃ）Ｍ＜Ｐ （Ｄ）不能确定
2．已知a,b是两个有理数, ab>a, a-b>b,对于下列三个结论：（1） a<1且b<1；（2） ab<0；（3）a≠0且b≠0. 正确的个数是（ ）.
（Ａ） 3 （Ｂ） 2 （Ｃ） 1 （Ｄ） 0
3．已知关于
的方程
的解满足
，则
的值是（ ）.
（Ａ）10或
（Ｂ）10或
（Ｃ）－10或 （Ｄ）－10或
4．已知：a>0，b<0，a<b<1那么以下判断正确的是（ ）.
（Ａ）1-b>-b>1+a>a （Ｂ）1+a>a>1-b>-b
（Ｃ）1+a>1-b>a>-b （Ｄ）1-b>1+a>-b>a
5．某轮船往返于A、B两地之间,设轮船在静水中的速度不变,那么,当水的流速增大时,轮船往返一次所用的时间( ).
（Ａ）不变 （Ｂ）增加 （Ｃ）减少 （Ｄ）增加、减少都有可能
6．用一副学生用的三角板的内角（内角为45°、45°、90°和30°、60°、90°），可以画出大于０°而小于176°的不同角的种数为（ ）.
（Ａ） 8 （Ｂ） 9 （Ｃ） 10 （Ｄ） 11
7．自然数
的各位数字之和记为S(n), 如n=38,S(n)=3+8=11,若对于某些自然数满足n-S(n)=2007, 则n的最大值是（ ）.
（Ａ）2025 （Ｂ）2023 （Ｃ）2021 （Ｄ）2019
8．甲乙两瓶里有两种药物 P,Q 的混合物. 其浓含量比为: 甲瓶中 P:Q=3:5, 乙瓶中 P:Q=3:7, 现从甲乙两瓶中各取若干克混合, 使得在取出的混合剂中, 药物 P 有 6 克, 药物 Q 有 12 克, 则从甲瓶中取出的混合剂的克数是( ).
（Ａ） ６ （Ｂ） ７ （Ｃ） ８ （Ｄ）９
9．用min(a,b)表示两数中的较小者，用max(a,b)表示a、b两数中的较大者，例如max(3,5)=5, min(3,5)=3, min(3,3)=3, max(5,5)=5,设a、b、c、d是互不相等的自然数，min(a,b)=p, min(c,d)=q, max(p,q)=x, max(a,b)=m, max(c,d)=n, min(m,n)=y,则（ ）.
（Ａ）x>y （Ｂ）x<y （Ｃ）x=y （Ｄ）x>y和x<y都有可能
10．对于数x，符号[ x ]表示不大于x的最大整数例如[ 3.14 ]=3, [－7.59]= －8则关于x的方程[
]=4的整数根有（ ）.
（Ａ）4个 （Ｂ）3个 （Ｃ）2个 （Ｄ）1个
二 填空题
11．咖啡A与咖啡B以x:y之比(以重量计)混合,A的原价为50元/千克,B的原价为4 元/千克,若A的价格增加10%,B的价格减少15%,则混合咖啡每千克的价格不变,则x:y= ．
12．设实数x、y满足
，则x+y＝ ．
13．某同学做一道代数题: “求代数式10x9+9x8+8x7+7x6+6x5+5x4+4x3+3x2+2x+1,当x=1时的值”,由于将式中某一项前的“+”号错看为“-”号,误得代数式的值为37, 那么这位同学看错了 次项前的符号.
14．已知 
中的每一个数的值只能取0、1、-2三个数中的一个，且满足：
，
，则
.
15．直角三角形的三边长分别是5，12，13，三角形内一点到三边的距离均为x，则x= .
16．将自然数按下列三角形规律排列,则第15行的各数之和是 .
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
……… ……… ……… ……… …………
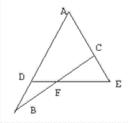
17．如图所示，已知AD：DB=5：2、AC：CE=4：3，則BF：FC=________.
18． 在1, 3, 5, ……, 2003这1002数的前面任意添加一个正号或一个负号，其代数和的绝对值最小值是 .
19．规定：n!=1×2×3×…×n. 那么 
除以2002的余数是 .
20．
四个足球队进行循环比赛(即任意两队将要作赛), 赛了若干场后, 
三队的比赛情况如下:
| 场数 | 胜 | 负 | 平 | 入球 | 失球 | |
| A队 | 2 | 0 | 2 | 0 | 3 | 6 |
| B队 | 2 | 1 | 0 | 1 | 4 | 3 |
| C队 | 3 | 2 | 0 | 1 | 2 | 0 |
| D队(答案): |
|
|
|
|
|
|
请在以上空格填入正确的数字.
三 解答题
21．在春节期间，某超市准备利用超大屏幕反复播放一个广告节目。这个广告节目每次播放时间是10秒钟。如果开始只有一段10秒的录象带母带。如果用两盘空白录象带在一台录象机互相转录，问应如何操作，才能用最少的录制遍数录制一盘可以播放一小时的广告节目？
22．如果可以将正整数1,2,3, …,n重新排成一数列，使得任意连续三项之和，都能被这三项中的第一项整除。如果这个数列的最末一项是奇数，试求 n的最大值，并写出所有满足条件的数列。
23．能不能将8×8的棋盘，分割为32个1×2或2 ×1的长方形，而且在每个长方形内只划一条对角线，使得这32条对角线中的任何两条对角线，都没有共同的端点？
参考答案
一． （1）B （2）C （3）A （4）D（5）B（6）D（7）D（8）C （9）D（10）B
二． （11）6：5 （12）3或6 （13） 8 （14） -37 （15） 2
（16）3390 （17） 2 （18） 14：15 （19）2001 （20）3，1，2，0，8
三 （20）操作方法如下：
第一步：将母带上的节目录入第一盘空白录象带；
第二步：将母带上的节目录入第二盘空白录象带；
第三步：将第一盘录象带带上的节目录入第二盘录象带；
第四步：将第二盘录象带带上的节目录入第一盘录象带；
如此反复，直到录到所需要的时间长度为止。
所录制的长度依次为1，1，2，3，5，8，13，21，34，55，89，144，233，377，……，
因为377>3600/10, 故操作14次就可以录制一盘可以播放一小时的广告节目。
（21）滿足題意的數列最長的長度是5。
如果數列
滿足題意，則不可能有連續二項是偶數，否則這二項之後的項都是偶數，題目要求最後一項是奇數。根據一個偶數後面一定要接二個或二個以上的奇數。除非接了一個奇數之後，整個數列就結束了。由於從
中奇數的個數比偶數的個數最多多一個。所以整個數列最多只有2個偶數，而且第一項是偶數，也就是偶奇奇偶奇。這樣我們用樹狀圖還可以找出所有滿足題意的最長數列出來。
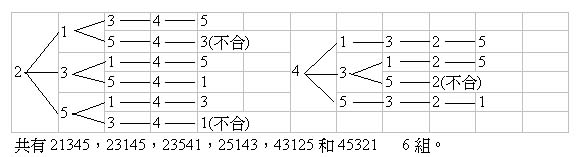
23．能，如下图
