初一数学（下）相交线与平行线单元过关题A
姓名： 学号：_____________
（满分100分，90分钟完卷）
一、填空题：（每小题3分，共30分）把每小题的正确答案填在各题对应的横线上。
1、两条不互相垂直的直线相交所成的4个角中，对顶角有_________________________对，邻补角有_________________________对，互补的角有_________________________对。
2、如图1，CD平分∠ACB，DE∥BC，∠AED＝800，那么∠EDC的度数为 。
3、如图2，AB∥CD，FE平分∠GFD，GF与AB交于H，∠GHA＝400，那么∠BEF的度数是 。
4、“一个角的邻补角相等”改写成“如果…，那么…”的形式后为
。
5、如图3，AD∥BC，∠DAC＝600，∠ACF＝250，∠EFC＝1450，则直线EF与BC的位置关系是 。
6、如图4，按虚线剪去长方形纸片相邻的两个角，并使∠1＝1200，AB⊥BC，则∠2的度数为 。
7、如图5，已知AB∥EF∥CD，且∠B＋∠BED＋∠D＝1960，∠B－∠D＝220，则∠BEF＝ 。
8、如图6，∠1＝820，∠2＝980，∠3＝800，则∠4＝ 。
9、如图7，已知MN⊥AB，MN⊥CD，垂足分别为G、H，直线EF分别交AB、CD于G、Q，∠GQD＝1300，则∠EGA－∠HGQ＝ 。
10、如图8，若AB∥DC，AD∥BC，则图中与∠A相等的角有 个。
二、选择题：各小题只有唯一一个正确答案，请将正确答案的代号填在题后的括号内（每小题3分，共30分）
11、下列说法正确的是（ ）
A、相等的角是对顶角 B、互补的两个角一定是邻补角
C、直角都相等 D、两条直线被第三条直线所截，同位角相等
12、张雷同学从A地出发沿北偏东500的方向行驶到B地，再由B地沿南偏西200的方向行驶到C地，则∠ABC的度数为（ ）
A、400 B、300 C、200 D、00
13、下列说法中，正确的是（ ）
A、相等的两个角是直角 B、同旁内角互补
C、一个角的补角一定是钝角 D、如果同位角不相等，两条直线一定不平行
14、如果a∥b，b∥c，那么a∥c，这个推理的依据是（ ）
A、等量代换 B、平行公理
C、两直线平行，同位角相等 D、平行于同一直线的两条直线平行
15、如图9，已知AB∥CD，AE⊥AB，BF⊥AB，∠C＝∠D＝1200，那么∠CBF是∠EAD的（ ）
A、5倍
B、
倍
C、4倍
D、
倍
16、如图10，如果AB∥CD，则
、
、
之间的关系是（ ）
A、
B、
C、
D、
17、如图11，下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角。其中正确的个数是（ ）
A、4个 B、3个 C、2个 D、1个
18、如图12，正方体ABCD－
中，
垂直于平面（ ）
A、
B、
C、
D、
19、下列说法错误的是（ ）
A、两条直线平行，内错角相等 B、两条直线相交所成的角是对顶角
C、两条直线平行，一组同旁内角的平分线到相垂直 D、邻补角的平分线互相垂直
20、一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的度数是（ ）
A、第一次右拐50°，第二次左拐130° B、第一次左拐50°，第二次右拐50°
C、第一次左拐50°，第二次左拐130° D、第一次右拐50°，第二次右拐50°
三、完成下面的证明推理过程，并在括号里填上根据（每空1分，本题共12分）
21、已知，如图13-1，∠1＝∠2，∠A＝∠F。求证：∠C＝∠D。
证明：∵∠1＝∠2（已知）
∠1＝∠3（对顶角相等）
∴∠2＝∠ （ ）
∴BD∥ （ ）
∴∠FEM＝∠D，∠4＝∠C （ ）
又∵∠A＝∠F（已知）
∴AC∥DF（ ）
∴∠C＝∠FEM（ ）
又∵∠FEM＝∠D（已证）
∴∠C＝∠D（等量代换）
22、已知，如图13-2，∠1＝∠2，CF⊥AB，DE⊥AB，求证：FG∥BC。
证明：∵CF⊥AB，DE⊥AB（已知）
∴∠BED＝900，∠BFC＝900（
）
∴∠BED＝∠BFC（等量代换）
∴ED∥FC（ ）
∴∠1＝∠BCF（ ）
又∵∠1＝∠2（已知）
∴∠2＝∠BCF（ ）
∴FG∥BC（ ）
四、计算与证明：（每小题6分，共18分）
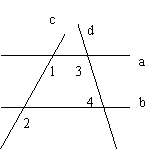
23、如图，已知：∠3=125°，∠4=55°，∠1=118°，
求：∠2的度数。
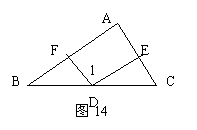24、已知，如图14，AC∥DF，∠1＝∠A。求证：AB∥DEA。
25、已知，如图15，∠ACB＝600，∠ABC＝500， BO、CO分别平分∠ABC 、∠ACB，EF是经过点O且平行于BC的直线，求∠BOC的度数。
五、做一做（本题6分）
26、已知△ABC、点D，过点D作△ABC平移后的图形，使点A移动到点D。
六、探索题（本大题共4分）
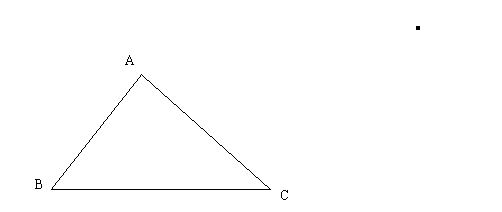
27、如图18，已知三角形ABC，求证：∠A＋∠B＋∠C＝1800。
分析：通过画平行线，将∠A、∠B、∠C作等角代换，使各角之和恰为一平角，依辅助线不同而得多种证法。
证法1：如图19，延长BC到D，过C画CE∥BA
∵BA∥CE（作图所知）
∴∠B＝∠1，∠A＝∠2（两直线平行，同位角、内错角相等）
又∵∠BCD＝∠BCA＋∠2＋∠1＝1800（平角的定义）
∴∠A＋∠B＋∠ACB＝1800（等量代换）
如图20，过BC上任一点F，画FH∥AC，FG∥AB，这种添加辅助线的方法能证明∠A＋∠B＋∠C＝1800吗？请你试一试。