七年级(下)数学期末模拟试卷
一、填空题（每题3分，共30分）
1、 在活动课上，小红已有两根长为4cm、8cm的小木棒，现打算拼一个等腰三角形，则小红应取的第三根小木棒长是＿＿＿＿＿
2、
的算术平方根是
3、如果
，那么
(填“＞”、“＜”、“＝”)
4、已知点P在第四象限，它的横坐标与纵坐标的和为2，则点P的坐标
为 （写出符合条件的一个点即可）
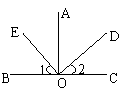
5、已知如图，AO⊥BC，DO⊥OE，∠1=56°，则∠2= 度。
 |
6、不等式
的非负整数解是
。
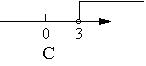
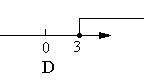
7、如图，∠ABC的平分线与∠ACB的外角平分线交于点D，若∠D＝60°，
则∠A＝ 度。
8、计算：
= 。
9、已知一多边形的每一个外角都等于72°，则它的内角和是
10、一张方桌由一个桌面和四条桌腿组成，如果1立方米木料可制作方桌桌面50个，或制作桌腿300条，现有5立方米木料，用多少木料做桌面，多少木料做桌腿，恰好全部制成方桌。设用
立方米木料做桌面，
立方米木料做桌腿，根据题意列方程组为
二、选择题（每题3分，共30分）
11、下列说法不正确的是（ ）
A、1的立方根是1 B、1的平方根是1
C、－1是1的平方根 D、0的算术平方根是0
12、在平面直角坐标系内，一个点向右平移2个单位后，又向下平移3个单位得到的点的坐标为（2，3），则该点原来的坐标为（ ）
A、（0，0） B、（3，6） C、（0，6） D、（6，0）
13、小刚设计了一个关于实数运算的程序：输入一个数后，输出的数总是比该数的平方小1，小刚按照此程序输入
后，输出的结果应为( )
A、1 B、2 C、3 D、4
14、某中学新科技馆铺设地面，已有正三角形形状地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则该校不应购买的地砖形状是( )
A、正方形 B、正六边形 C、正八边形 D、正十二边形
15、二元一次方程
的正整数解的组数有( )
A、一组 B、二组 C、三组 D、四组
16、方程
的和
的公共解是（ ）
A、
B、
C、
D、
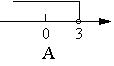
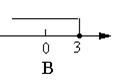
17、在数轴上表示
正确的是( )
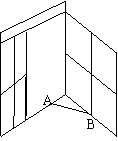18、如图，窗户打开后，用窗钩AB可将其固定，所运用的几何原理是( )
A、三角形具有稳定性 B、两点确定一条直线
C、垂线段最短 D、 两点之间线段最短
 |
1
19题图 18题图
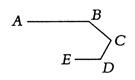
）19、如图，是赛车跑道的一段示意图，其中AB∥ DE，测得
∠B=140°, ∠D＝120°，则∠C的度数为（ ）
A．120° B．100° C．140° D．90°
20、图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（ ）
A 25 B 66 C 91 D 120
 |
三、解答题（共60分）
21、（8分）解方程组
22、(8分)解不等式组，并把解集在数轴上表示出来。
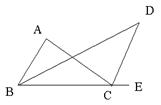
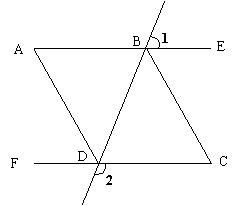
23、（8分）已知：如图，∠1 = 60°，∠2 = 120°，∠A =∠C，DA平分∠BDF，试说明：BC平分∠DBE。
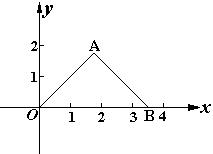
24、（8分）如图,
已知△OAB在平面直角坐标系中的坐标分别是A(,)、B(2, 0).
(1)求△OAB的面积;
(2)把△OAB向左平移个单位后, 三个顶点坐标分别是多少?
25、(8分)如图, 填空：
①
∴ // （ ）
②∵ //
∴
(
)
∵_______ // ________
∴∠A＋∠ABC=180°( )
∴______=_______ ( )
26、(10分)班长问老师要分成几个小组，老师风趣地说
27、(10分)对优质教育的需求某中学决定改变条件，计划拆除一部分校舍、建造新校舍．拆除旧校舍每平米需80元，建造新校舍每平米需700元．计划在年内拆除旧校舍与建造新校舍共7200平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的80％，而拆除校舍则超过了10％，结果恰好完成了原计划的拆、除的总面积
（1）求原计划拆建面积各多少平方米？
（2）若绿化1平方米需200元，那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米？