数学七年级（下）第五章《三角形》单元测验
班级：____________姓名：___________分数：_________________
一、填空题（每空2分，共30分）
1、 写出图中以AB为边的三角形_____________________________________________.
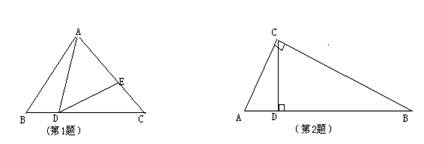
2、 已知，如图，∠ACB=90°，CD⊥AB，垂足为D
（1） 图中有_________个直角三角形，它们是_____________________________;
（2） ∠A=________，理由是___________________________________________.
3、 已知△ABC中，∠A=70°,∠B=∠C,则∠C=___________.
4、 已知△ABC中，∠A-∠B=∠C,则∠A=___________.
5、 已知AD是△ABC的角平分线，∠BAC=80°,则∠BAD=__________.
6、 已知AE是△ABC的中线，BE=5cm,则BC=____________.
7、 已知三角形的两边分别为2cm和5cm，则第三边c的取植范围为_______________.
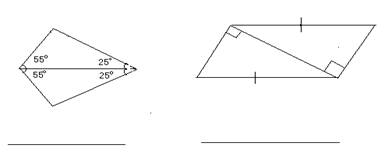
8、 分别写出下列三角形全等的根据：
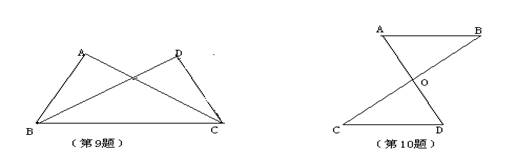
9、 如图，△ABC≌△DCB，其中∠ACB与∠DBC是对应角，则AC=________，∠ABC=_________.
10、 如图，AB∥CD，AO=DO，AB=6cm，BO=4cm，则CD=____________.
二、选择题（每题3分，共24分）
1、下面是四组线段的长度，哪一组能组成三角形（ ）
A、2，2，4 B、5，5，5 C、11，5，6 D、3，8，24
2、下面哪一条线段能把三角形分成面积相等的两个三角形（ ）
A、角平分线 B、中线 C、高 D、以上都不是
3、下列说法错误的是（ ）
A、
三条边对应相等的三角形全等
B、 两个角及夹边对应相等的三角形全等
C、 两边及夹角对应相等的三角形全等
D、 两条边及一角对应相等的三角形全等
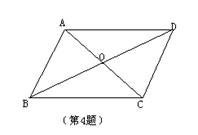
4、如图，已知AC与BD相交于点O，AO=CO，
BO=DO，图中有几对全等三角形（ ）
A、2 B、3 C、4 D、5
5、已知△ABC中，∠A=50°，∠B=60°，则△ABC是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形
6、下列说法错误的是（ ）
A、 三角形中至少有两个锐角
B、 锐角三角形中任意两个锐角的和大于90°
C、 三角形的三个内角的比为1：2：3，则它是直角三角形
D、面积相等的两个三角形全等
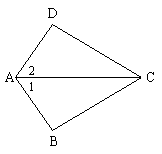
7、如图，∠BAC=∠DAC下列哪个条件不能使得△ABC≌△ADC（ ）
A、AB=AD B、BC=DC C、∠B=∠D D、∠BCA=∠DCA
8、如图，AB=CD，∠BAE=∠DCF，BD=8，EF=4，则BE=（ ）
A、4 B、8 C、2 D、12
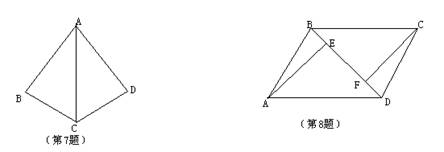
三、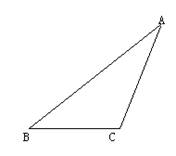
作图题（10分）
1、 如图，作出△ABC的BC边上的高。（4分）
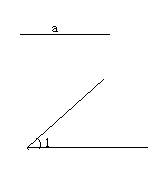
2、 已知线段a和∠1，作一个△ABC，使得AB=a，AC=2a，∠A=∠1.（6分）
四、解答题（36分）
1、（6分）如图，已知
，AD=AB，求证：
。
2、（6分）如图，在
中，AD平分
，交BC于D，
，
。求
的度数。
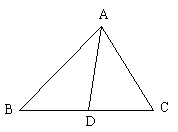
3、 （8分）如图，点A、D、C、F在同一条直线上，AB=FE，AD=CF，∠A=∠F；
问：∠B与∠E相等吗？试说明理由。
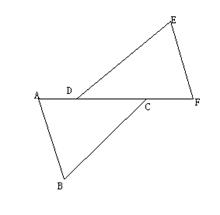
4、（8分）如图，△ADB≌△EDB， △BDE≌△CDE， B、E、C在一条直线上。
（1） BD是∠ABE的角平分线吗？为什么？
（2） DE⊥BC吗？为什么？
（3） 点E平分线段BC吗？为什么？
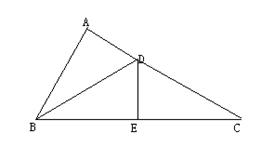
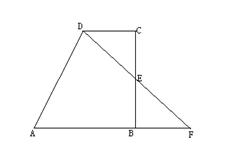
5、 如图，BC⊥CD，BC⊥AB，E为BC的中点，DE的延长线交AB的延长线于点F。AF与AB+CD相等吗？为什么？（8分）
答案：
一、填空题
1、 △ABD，△ABC
2、 （1）3，Rt△ABC、Rt△ACD、Rt△BCD
（2）∠BCD，同角的余角相等
3、55°
4、90°
5、40°
6、10cm
7、3cm<c<7cm
8、ASA，HL
9、BD，∠DCB
10、6cm
二、选择题
1、B 2、B 3、D 4、C 5、A 6、D 7、D 8、C
三、作图题（略）
四、解答题
1、（略）
2、∠ADB=105°°
3、 相等。由AB=FE，∠A=∠F，AC=FD可得△ABC≌△EFD，从而可得∠B=∠E。
4、 （1） 是。∵△ADB≌△EDB，∴∠ABD=∠EBD
（2）是。∵△BDE≌△CDE，∴∠DEB=∠DEC=
×180°=90°
（3）是。∵△BDE≌△CDE，∴BE=CE
5、相等。由∠DCE=∠FBE，CE=BE，∠CED=∠BEF可得△DCE≌△FBE，从而CD=BF；故AF=AB+BF=AB+CD。