九年级数学测试题
班级 姓名 得分
一、选择题。(每小题3分,共24分)
1、下列命题中,假命题的是( )
A、两个锐角相等的两个直角三角形全等
B、斜边及一锐角对应相等的两个直角三角形全等
C、两条直角边对应相等的两个直角三角形全等
D、一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等
2、有一两边长分别为5cm和6cm的等腰三角形的周长是( )
A、16cm B、17cm C、16 cm或17cm D、11cm
3、设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列选项中能表示它们之间的关系的是( )
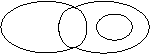
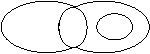
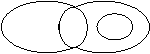
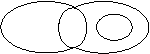 |
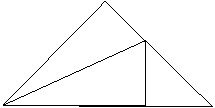
4、如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=10cm,则△DEB的周长为( )
 A、4cm
A、4cm
B、6cm
C、8cm
D、10cm
5、等腰三角形底边长为7,一腰上的中线把其周长分成两部分的差为3,则腰长是( )
A、4 B、10 C、4或10 D、以上答案都不对
6、已知2是关于x的方程 的一个根,则2a-1的值是( )
A、3 B、4 C、5 D、6
7、三角形两边的长分别是8和6,第三边的长是一元二次方程x2-16x+60=0的一个实数根,则该三角形的面积是( )
A、24 B、24或 C、48 D、
8、下列说法中,正确的是( )
A、方程2x2+6=0有两个解x=±3
B、方程x(x+3)=2(x+3)中,两边都除以(x+3),得x=2
C、方程(m+1)x2+mx-1=0,当m=1时,该方程是一元一次方程
D、一元二次方程ax2+bx+c=0中,b、c可以为零,但a不能为零
二、填空题(每小题3分,共36分)
9、如果代数式x2-5x+10的值是4,则x= 。
10、某商品原价为400元,连续两次降价后为324元,那么平均每次降价的百分率为 。
11、方程x2+6x-5=0配方后得方程( )
A、(x+3) 2=14 B、(x-3)2=14 C、(x+6)2= D、以上答案都不对
12、若a的值使x2+4x+a=(x+2)2-1成立,则a的值是 。
13、设(m+2)x+3mx+1=0是关于x的一元二次方程,则m= 。
14、如图,AC平分∠PAQ,
点B、B′分别在边AP、AQ,
要使AB=A B′,则可补充的
一个条件为 。
15、在△ABC中,AB=5cm,BC=6cm,BC边上的中线AD=4cm,则∠ADC的度数是 。
16、如图,∠E=∠F=90°,∠B=∠C,
AE=AF,给出下列结论:①∠1=∠2,
②BE=CF,③ACN≌ABM,④CD=DB,
其中正确的结论是:
17、如图,在Rt△ABC中,∠B=90°,
∠A=40°,AC的垂直平分线MN与AB
交于点D,则∠BCD= 。
18、等腰三角形的周长为11,腰长为偶数,则它的底边长为 。
19、到三角形三边所在直线距离相等的点有 个。
20、设方程x2+3x-4=0的两根分别为x1,x2,则x1+x2= ,x1·x2= 。
三、解答题。(共60分)
21、用配方法解方程:2x2-4x+1=0(5分)
22、用公式方解方程:
23、用分解因式法解方程3(4x2-9)=2(2x-3)(5分)
24、如图,一辆汽车在公路AB上由A向B行驶,M、N分别是位于公路AB两侧的村庄,在公路AB上是否存在点P,使汽车行驶到该点时,与M、N的距离相等?如果存在,请画出这一点P(保留作用痕迹,不写画法),如果不存在,请简要说明理由。(6分)
25、如图,DE是△ABC的AB边的垂直平分线,分别交AB、BC于D、E,AE平分∠BAC,若∠B=30°,求∠C的度数。(6分)
26、将进货单价为40元的商品按50元出售时能卖500个,已知该商品要涨价1元,销售量就要减少10个,为了获得8000元利润,售价应定为多少,这时应进货为多少个?(10分)
27、如图,△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动。
(1)如果P、Q分别从A、B同时出发,经几秒钟,△PBQ的面积等于8cm2?(5分)
(2)如果P、Q分别从A、B同时出发,并且P到B点后又继续在BC边上前进,Q到C点后又继续在CA边上前进,经几秒钟,使△PCQ的面积等于12.6cm2?(6分)
 | |||
 | |||
28、某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80m,BC=60m。
(1)若入口E在边AB上,且与A、B等距离,求从入口E到出口C的最短路线的长;
(2)若线段CD是一条水渠,且D点在边AB上,已知水渠的造价为10元/米,则D点在距A点多远处时,此水渠的造价最低?最低造价是多少?