|
一填空题(每题4分，共40分)
1电视塔在学校的正北方向，那么学校在电视塔的__________的方向上。
2若x=2是方程3x+4=
-a的解，则a2-
的值是__________
3由四舍五入得到的近似数3.1万,精确到________,有___________个有效数字.
4若
互为相反数，则x的值是________
5某商品进价为300元，按标价的六折销售时，利润为5%，求商品的标价为____元。
6已知一条射线OA，若从O点再引两条射线OB和OC，使∠AOB=600，∠BOC=600，则∠AOC的度数为___________.
7将一个长方体的表面沿某些棱剪开，展成一个平面图形，至多可以剪 ____几条棱。
8 如图，折叠围成一个正方体时，数字_____会在与数字4所在的平面相对的平面上。
9如下图，是一个由若干个长、宽、高相等的小正方体摆成的几何体，从正面看、从左面看、从上面看的平面图，则组成这个几何体共用_________个小正方体。
|
|
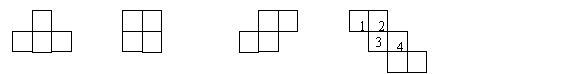
正面 左面 上面 (第8题)
10观察下列等式:1+3=
，
，
按规律填空,1+3+5+7+9+
+99=____________.
二选择题 （每题5分，共40分）
1在一扇形统计图中，其中一个扇形的园心角为1350，那么这部分占总体的百分比为( )
A 50% B 30% C 35% D 37.5%
2某粮店出售三种品牌的面粉,袋上分别标有质量为(25
0.1)kg、（250.2）kg
(25 03)kg的字样，从中任意拿出两袋 ，它们的质量最多相差( )
A 0.8kg B 0.6kg C 0.5kg D 0.4kg
2已知
=0，则xyz的值是
A 负数 B 非负数 C 正数 D 非正数
A 唯一确定的值 B 2种不同的值 C 3种不同的值 D 4种不同的值
4若n为自然数，则10n表示的数是（ ）
A 10个n相乘所得的积 B 1后面有n个零
C 1后面有(n-1)个零 D 1后面有(n+1)个零
5下列图形中，不是正方体展开图的是( )
A B C D
6在一个停车场内有24辆车，其中汽车有4个轮子，摩托车有3 个轮子，且停车场上只有汽车和摩托车，这些车共有86个轮子，那么摩托车应为( )
A 14辆 B 12辆 C 16辆 D 10辆
7某人从家里去上班，每小时行5千米，下班按原路返回时，每小时行4千米，结果下班返回比上班多花10分钟，设上班所用时间为t小时，则可列方程( )
A 5t=4(t-
B 5(t-
C 5(t+ D 5t=4(t+
)
8 现定义两种运算：“ 
”，“ 
”，对于任意两个整数a、b，a b=a+b-1，
a b=ab-1，那么4 [（6 8（3 5）]=
（ ）
A 102 B 103 C 104 D 105
三解答题（12分+12分+10分+12分+12分+12分，共70分）
1电器商场销售一种高档商品,该商品的标价是12000元,为了促销,销售部经理做了两个方案(1)将该商品进行八折销售;(2)不打折销售,实行“买一送一”的方式进行销售，即买一件该商品，就送一台标价为2600元的彩电，而这种彩电的成本价为1800元。如果你是该商场的经理，你会选择哪个方案？说说你的理由。
2某城市出租车收费标准如下：不超过2km收费3元;超过2km的部分，每千米收费1.2元,
(1)若行驶xkm(x>2),试用含x的代数式表示应收的车费;
(2)某人乘坐出租车行驶5km应付多少元?
(3)若某人付车费15元,出租车行驶了多少千米?
 |
3计算：（-1）+（-1）2+（-1）3+…+（-1）99+（-1）100+
4 有若干个数，第一个数记为a1，第二个数记为a2，第三个数记为a3…，第n个数记为an，若a1=1/2，从第二个数起，每个数都等于“1与它前面的那个数的差的倒数”。
（1）试计算：a2=_______,a3=_________,a4=__________.
(2)根据以上结果,请你写出:a1998=_________,a2000=__________.
5给出依次排列的一列数：-4,8，-16，32，-64,128……
(1)试按照这个数排列的某种规律，继续写出后面的两项；
(2)这一列数的第n个数是什么？第10个数呢？
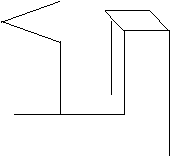
5如图,是物体的直观图,请你画出从正面看、从左面看、从上面看的平面图形.
‘’
