初一数学
期期中考试试卷
得分_________
说明：考试时间90分钟，满分100分.
一、细心填一填：可别填错啦！（每空2分，满分40分）
1．若＋3米表示向南行走3米， 则－7米表示__________________.
2．－1的相反数是 , 倒数是 ， 绝对值是 .
3．计算：(－6)＋15＝_________， (－1.7)－(－2.5)＝_________.
4．比较大小（用“＜”或“＞”或 “＝”号填空）
（1）－(－3)_________－－3； （2）－3_________－0.033.
5．已知x＝3，y＝2，且xy＜0，则x＋y＝_______.
6．（1）一只苍蝇腹内的细菌约有2800万个，这个数据用科学记数法可以表示为：___ ___万个；
（2）0.035449≈ （保留两个有效数字）.
7．为了搞促销，超市规定购买不超过50元的商品，按全额收费，购买超过50元的商品，超过部分按九折收费，某顾客有一次购买商品付了212元，实际上他这次购买的商品的价值是_________ 元.
8．单项式－2x2y的系数是_________，次数是_________.
9．多项式3x2y－7x4y2－xy3＋是________次四项式，最高次项的系数是_________，按x的降幂排列为___________________________.
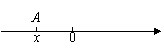10．如图所示，数轴上的点A所表示的数是x，则点A到原点的距离是 .
11．给出－1、6、－8、2四个数，对它们进行有理数的混合运算，使运算结果是24（每个数只能用一次），列出你的算式：___________ ____.
12．观察下列等式：9－1＝8，16－4＝12，25－9＝16，36－16＝20，……这些等式反映出自然数间的某种规律. 设n表示自然数，试用关于n的等式表示出你所发现的规律：__________ ____.
二、认真选一选：每题有且只有一个正确答案（每题3分，满分18分）
13．下列结论中正确的是 （ ）
A．0既是正数，又是负数 B．0是最小的正数
C．0是最大的负数 D．0既不是正数，也不是负数
14．下列运算：①
； ②
；③－14＝4；④－(－0.1)3＝0.001中，错误的个数为
（ ）
A 2个 B 3个 C 4个 D 5个
15．由四舍五入得到的近似数是36，下列哪些数可能是原来的数 （ ）
（1）35.48 （2）35.88 （3）36.09 （4）36.48
A．（1）（2）（3） B．（2）（3）（4）
C．（1）（2）（4） D．（1）（3）（4）
16．若有理数a、b满足＝2006，则必有 （ ）
A．a＞b B．a＜b C．a＞b D．a＞b
17．报告厅第一排有n个座位，后面每排比前一排多一个座位，则第m排的座位的个数是 （ ）
A．m＋1 B．n＋m C．n＋(m－1) D．n＋(m＋1)
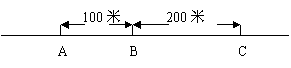18．某公司员工分别住在A、B、C三个住宅区，A区有30人，B区有15人，C区有10人，三个区在一直线上（如下图所示），公司的接送车打算在此间只设一个停靠点，为要使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应在 （ ）
A．A区 B．B区 C．C区 D．A、B两区之间
三、解答题（本题共7大题，满分42分）
19．计算：（每小题4分，共16分）
①1＋(－1)－(－)－(＋)； ②( － )×(－24)；
③－23÷×(－ )； ④×( － )÷.
20．（4分）某升降机第一次上升6米，第二次又上升4米，第三次下降5米，第四次又下降7米，升降机共运行了多少米？这时升降机在初始位置的上方还是下方，相距初始位置多少米？
21．（4分）已知(a＋2)2＋b－3＝0，求(a－b)2的值.
22．（3分）如果用一般方法计算：7778×9999＋3333×6666非常繁琐，但如果综合运用结合律、分配律，可以用下面方法简化计算：
原式＝7778×9999＋9999×2222
＝9999×(7778＋2222)
＝9999×10000
＝
你能用类似的方法计算9999×1111＋3333×2223＋6666×2222吗？
23．（4分）对于两个有理数a、b，我们规定运算“★”：a★b＝a－b＋ab，试求：－1★(2★3)的值.
24．（5分）已知关于x、y的单项式－xmy3与3x1－nyp的和是一个五次单项式，试求代数式7mn－2mp－5mn＋6mp－5mnp的值.
25．（6分）某商场计划投入一笔资金采购一批紧销商品，经过市场调查发现，如果月初出售，可获利15%，并可用本金和利润再投资其他商品，到月末又可获利10%；如果月末出售可获利30%，但要付出仓储费用700元.
（1）若商场投资x元，分别用x的代数式表示月初出售和月末出售所获得的利润.
（2）若商场投资40000元，问选择哪种销售方式获利较多？此时获利多少元？