初一数学上学期期终试卷
一、选择题
1．据中新社报道：2010年我国粮食产量将达到540 000 000 000千克，用科学记数法表示这个数为（ ）
（
）5.4×1010千克 （
）5.4×1011千克 （
）54×1010千克 （
）0.54×1012千克
2、下列运算中，正确的是（ ）
（）
（）
（）
（）
3、 国家规定：存款利息税=利息×20%，银行一年定期储蓄的年利率为1.98%.小明有一笔一年定期存款，如果到期后全取出，可取回1219元。若设小明的这笔一年定期存款是x元，则下列方程中正确的是（ ）
（）
（）
（）
（）
4、下列图形中可能错误的是（ ）
（）过一点有且只有一条直线与已知直线平行；（）过一点有且只有一条直线与已知直线垂直；
（）两条直线相交，有且只有一个交点；（）若两条直线相交所成直角，则这两条直线互相垂直。
|
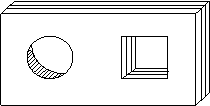
6、如下右图，把一个长方形纸片沿EF折叠后，点D、C分别落在D/、C/的位置，若∠EFB=65°，
则∠AE D/等于（ ）
（）50° （）55° （）60° （）65°
7、观察下列算式：
，
，
，
，
，
，
，
……
根据上述算式中的规律，你认为
的末位数字是
（ ）
（）2
（）4
（）6
（）8
8、在数轴上与原点的距离等于2个单位的点表示的数是（ ）
（）2 （）－2 （）－1和3 （）－2和2
9、如图是一块带有圆形空洞和方形空洞的小木板，则下列物体中既可以堵住圆形空洞，又可以堵住方形空洞的是（ ）
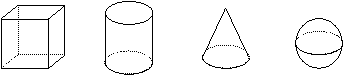
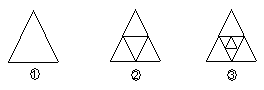
（A） (B) (C) (D)
10、图①是一个三角形，分别连接这个三角形的中点得到图②；再分别连接图②中间小三角形三边的中点，得到图③。按上面的方法继续下去，第
个图形中有
个三角形（用含字母的代数式表示）。
二、填空题
1． 的相反数是4；—5倒数是 ， 的绝对值是3。
2、
、
是数轴上的二个点，线段
的长度为3，若点表示的数为﹣1，则点表示的为
。
3、一根长长的电线上停了三只小鸟，我们可以近似地看作一条直线上有三个点、、（如图所示）
（1）请写出图中所有的线段，他们分别是 ；
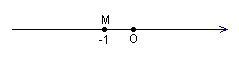
（2）若点是线段
的中点，
，则
。
4、华氏温度
（℉）与摄氏温度
（℃）之间存在着如下的关系：
。如果某地某天早晨的摄氏温度为5℃，那么此地这天早晨的华氏温度是
℉。
5、用“数字牌”做24点游戏，抽出的四张牌分别表示2、－3、－4、6（每张牌只能用一次，可以用加、减、乘、除等运算）请写出一个算式，使运算结果为24： 。
6、七点三十分时，钟表上时针与分针的夹角为 °，可化为 ′。
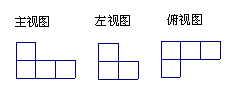
7、下面是由一些相同的小正方形构成的几何体的三视图，那么这些相同的小正方体的个数是 。
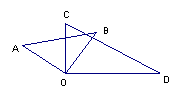
8、如图，将一副三角板的直角顶点重合，摆放在桌面上。若∠AOD=145°，则∠BOC= °
三、计算与解方程
1．
；
2．化简：
3、解方程：
4、先化简，再求值：
四、解答题
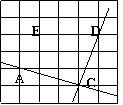
1、如图，在方格纸中，直线AC与CD相交于点C.
⑴ 过点E画直线EF，使EF⊥AC；
⑵ 分别表示（1）中三条直线之间的位置关系；
⑶ 根据你观察到的EF与CD间的位置关系，用一句话来解释你的结论.
2、在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形，折成一个无盖的长方体。
⑴如果剪去的小正方形的边长为xcm，请用x来表示这个无盖长方体的容积；
⑵当剪去的小正方体的边长x的值分别为3cm和3.5cm时，比较折成的无盖长方体的容积的大小。
3、据电力部门统计，每天8︰00至21︰00是用点高峰期，简称“峰时”，21︰00至次日8︰00是用电低谷期，简称“谷时”。为了缓解供电需求紧张的矛盾，我市电力部门拟逐步统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表：
| 时间 | 换表前 | 换表后 | |
| 峰时（8︰00—21︰00） | 谷时（21︰00—8︰00） | ||
| 电价 | 每度0.52元 | 每度0.55元 | 每度0.30元 |
小明家对换表后最初使用的95度电进行测算，经测算比换表前使用95度电节约了5.9元，问小明家使用“峰时” 电和“谷时” 电分别是多少度？
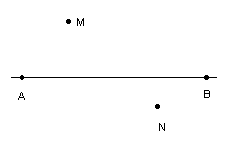
4、如图，一辆汽车在直线形的公路AB上由A向B行使，M、N分别是位于公路AB两侧的村庄。
⑴设汽车行使到公路AB上点P位置时，距离村庄M最近；行使到点Q位置时，距离村庄N最近。请你在图中公路AB上分别画出点P、Q的位置。（保留画图痕迹）
⑵当汽车从A出发向B行使时，在公路AB的哪一段上距离M、N两村都越来越近？在哪一段上距离村庄N越来越近，而离村庄M却越来越远？（分别用文字语言表示你的结论，不必证明）
⑶在公路AB上是否存在这样一点H，使汽车行使到该点时，与村庄M、N的距离相等？如果存在，请在图中AB上画出这个点（保留画图痕迹，不必证明）；如果不存在，请简要说明理由。
5、．先填表，并回答问题：
| x | －2 | －1 | 0 | 1 | … |
| 5x－12 | … | ||||
| 3x－5 | … |
⑴随着x的值的逐渐增大，两个代数式的值如何变化？
⑵猜猜看，若x的值逐渐增大，哪个代数式的值先到达13？用你学到的知识和方法解释你的判断。
⑶想一想，x在什么范围时，一定有5x－12的值大于3x－5？
五、探究与思考
1、若干张扑克牌被平均分成三份，分别放在左边、中间、右边。（每堆至少2张）
按以下顺序操作：首先从左边一堆中拿出两张放进中间一堆中，然后从右边一堆中拿出一张放进中间一堆中，最后从中间一堆中拿出一些牌放到左边，使左边的张数是最初的2倍。
⑴按以上方法操作结束后，若左边所剩扑克牌比右边所剩扑克牌多10张，求原来每份牌有几张？
⑵小明认为：无论一开始每份是几张牌，最后中间一堆总剩1张扑克牌。你同意他的看法吗？说出你的理由。
2、张老师骑摩托车的速度为每小时45千米，学生步行的速度是每小时5千米，学校与车站相距15千米。如果2名学生要在55分钟内从学校到车站，请张老师用摩托车送，但摩托车后座只能坐一人，学生不能驾车，请你设计一个方案（学生只能步行或乘摩托车，上下摩托车的时间不计），使2名学生能在55分钟内全部到达车站，并用方程的有关知识说明理由。
（如果方案能使2名学生在规定时间内全部到达车站，时间少于47分钟可得7分，时间在47—55分钟以内的可得5分）
你的方案是：
理由及解答：