七年级第二学期中试卷
学号 班级 姓名
一、 选择题。（每题2分共36分）
1、下列说法正确的是……………………………………………………………( )
A.周长相等的两个三角形全等 B.面积相等的两个三角形全等
C.三个角对应相等的两个三角形全等 D.三条边对应相等的两个三角形全等
2、下列各组线段能组成三角形的是……………………………………………( )
A.3cm，3cm，6cm B.7cm,4cm,5cm C.3cm,4cm,8cm D.4.2cm,2.8cm,7cm
3、将如图图案绕中心O按逆时针旋转90O,得到的图案是: ……………………( )
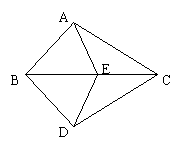4、如图，把图形沿BC对折，点A和点D重合，那么图中共有全等三角形……………(
)
A.1对 B.2对 C.3对 D.4对
5、在一个装有黑色围棋的盒子中摸出一颗棋子，
摸到一颗白棋是………………( )
A.必然事件 B.不确定事件
C.不可能事件 D.无法判断
6、下列条件中，不能判定三角形全等的是……………………………………( )
A.三条边对应相等 B.两边和一角对应相等
C.两角和其中一角的对边对应相等 D.两角和它们的夹边对应相等
7、下列各组中,两个图形是通过平移变换得到的是: …………………( )
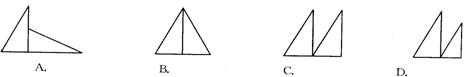
8、掷一枚均匀的骰子，骰子停止转动后朝上一面的点数出现以下情况的概率最小的是…………………………………………………………………………………( )
A.偶数 B.奇数 C.比5小的数 D.数6
9、如图,某同学把一块三角形的玻璃打碎成三片,现在他
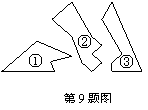要到玻璃店去配一块与原来相同的玻璃.那么最省事的办法是
带( )去配。
A、① B、② C、③ D、①和②
10、下列说法中错误的是…………………………………………（ ）
A、三角形三条角平分线都在三角形的内部
B、三角形三条中线都在三角形的内部
C、三角形三条高都在三角形的内部
D、三角形三条高至少有一条在三角形的内部
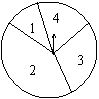
11、如图是一个可以自由转动的转盘，转动这个转盘，当它停止转动时，
指针最可能停留的区域是………………………………………( )
A.1 B. 2 C. 3 D. 4
12、锐角三角形中，最大角α的取值范围是（ ）
A、0o＜α＜90oº B、60o＜α＜90oº C、60o＜α＜180oº D、60oº≤α＜90o
13、已知三角形的三边分别为2，
，4那么
的取值范围是（ ）
A、
B、
C、
D、
14、如右图，已知△ABC≌△DEF，若∠A=∠D，BE=6，BC=4，
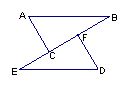则CF等于…………( )
A、4
B、3
C、2
D、不能确定
15、
 |
16、 如图，已知△ABC中，∠B=45°，∠C=75°，AD是BC边上的高，
AE是∠BAC的平分线，∠DAE=（ ）度。
A、15 B、30 C、45 D、25
17、等腰三角形的一边等于3，一边等于6，则它的周长等于（ ）
A、12 B、12或15 C、15或18 D、15
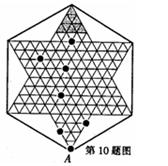18、右图是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子，我们约定跳棋游戏的规则是：把跳棋棋子在棋
盘内沿直线隔着棋子对称跳行，跳行一次称为一步。已知点A为己方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最小步数为（ ）
A、2步 B、3步 C、4步 D、5步
二、 填空题。（每空2分共42分）
19、“小小竹排水中游，巍巍青山两岸走”，所蕴涵的图形变换是__________变换。
20、在△ABC中，∠A＋∠B=1100，∠C＝2∠A，则∠A= ，∠B= .
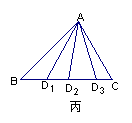
21、如下图，甲、乙、丙中分别有__ ___、__ ___、__ ___个三角形；
若在△ABC的边BC上任取n个点，则有___ __个三角形。
22、为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的理由是 __ ．
23、从装有8个红球、2个白球的袋子中随意摸出一个球，摸到可能性较小的是 球.
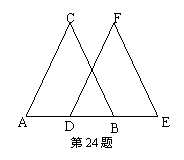24、如图，△ABC≌△DEF,点B和点E, 点A和点D是对应顶点，则AB= ，CB= ,
∠C= ,∠CAB= .
25、正方形有 条对称轴，圆有 条对称轴.
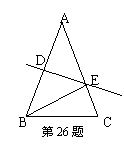
26、如图，△ABC中，AB=AC=13cm，AB的垂直平分线交AB于D,
交AC于E,若△EBC的周长为21cm,则BC= cm.
27、一批成品运动鞋共100双，其中次品5双.从中任选一双运动鞋，
是次品的概率是
.
28、把一个长方形作相似变换，各条边放大到原来的3倍，则放大后
的新长方形的周长是原长方形的 倍，新长方形的面积是原长
方形面积的 倍.
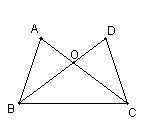
29、如图，已知AC＝BD，要使得ΔABC≌ΔDCB，只需增加
|
30、如上图,映在镜子里的号码的实际号码是 .
三、 解答题。（共42分）
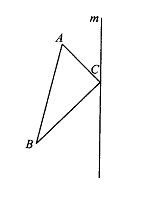
31、(6分)已知ΔABC和直线m,以直线m为对称轴,画ΔABC经轴对称变换后所得的图形.
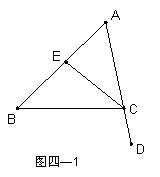32、(8分)如图（四—1）在△ABC中，∠B=40
，∠BCD=100，EC平分∠ACB，求∠A与∠ACE的度数。
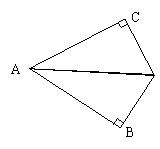33、(8分)已知AD平分∠CAB,且DC⊥AC, DB⊥AB，那么AB和AC相等吗？请说明理由.
|
34、（10分）如图，在△ABC和△DEF中，∠A=∠D，AC=DF，AE=BD，则∠C=∠F。请说明理
由（填空）。
解：∵AE=BD（ ）
∴AE-BE= -BE。
∴AB=DE
在△ABC和△DEF中，
= ，
= ，
= ，
∴△ABC≌△DEF（ ）
∴∠C=∠F（ ）
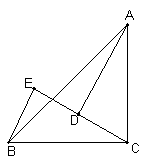35、（10分）如图，在ΔABC中，已知∠ACB＝90º，CA＝CB，AD⊥CE于点D，BE⊥CE于点E，说出AD＝CE的理由．
七年级第二学期第一阶段学能测试答卷座位号
学号 班级 姓名 得分
一、选择题。（每题2分共36分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
二、填空题。（每空2分共42分）
19、 20、 ， 21、 ， ， ，
22、 23、
24、 ， ， ， 25、 ，
26、 27、 28、 ，
29、 30、
三、解答题。（共42分）
31、(6分)已知ΔABC和直线m,以直线m为对称轴,画ΔABC经轴对称变换后所得的图形.
32、(8分)如图（四—1）在△ABC中，∠B=40，∠BCD=100，
EC平分∠ACB，求∠A与∠ACE的度数。
33、(8分)已知AD平分∠CAB,且DC⊥AC, DB⊥AB，那么AB和AC相等吗？请说明理由.
 |
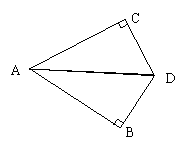34、（10分）如图，在△ABC和△DEF中，∠A=∠D，AC=DF，AE=BD，则∠C=∠F。请说明理由（填空）。
解：∵AE=BD（ ）
∴AE-BE= -BE。
∴AB=DE
在△ABC和△DEF中，
= ，
= ，
= ，
∴△ABC≌△DEF（ ）
∴∠C=∠F（ ）
35、（10分）如图，在ΔABC中，已知∠ACB＝90º，CA＝CB，AD⊥CE于点D，BE⊥CE于点E，说出AD＝CE的理由．