第四章 图形的初步认识(一)
班级________姓名_____________
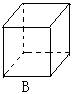
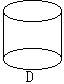
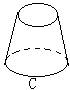1、下列图形中为圆柱体的是（
）
2、将n边形的一个顶点与其他（不相邻的）连结起来，这样的对角线的条数为（ ）
A．
B．
C．
D．
3、若一个立体图形的正视图与左视图都是等腰三角形，俯视图是圆，则这个图形可能是（ ）
A．圆台 B．圆柱 C．圆锥 D．三棱锥
4、一个多边形至少可以分割成5个三角形，则这个多边形的边数为（ ）
A．5 B．6 C．7 D．8
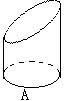
5、一只蚂蚁从如图1的正方形的一顶点A沿着棱爬向B，只能经过三条棱，共有多少种走法（ ）
A．8种 B．7种 C．6种 D．5种
6、在下面图形中，不能折成正方体的是（ ）
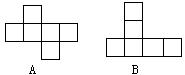
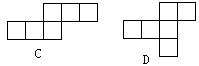
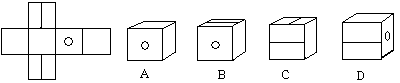
7、如图，把左边的图形折叠起来，它会变为 （ ）
8、下面图形经过折叠不能围成棱柱的是 （ ）
 |
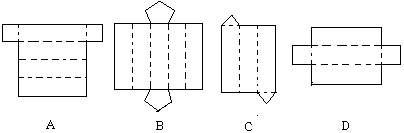
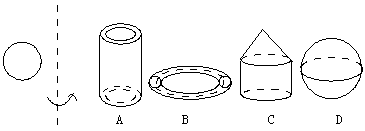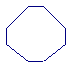
9、如图把一个圆绕虚线旋转一周，得到的几何体是（ ）
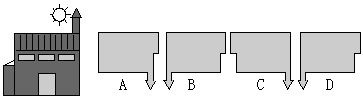
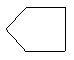
10、如图，太阳在房子的后方，那么房子在地面上的影子是（ ）
 |
11、一个几何体的边面全部展开后铺在平面上，不可能是 （ ）
A.一个三角形 B.一个圆 C.三个正方形 D.一个小圆和半个大圆
12、用一个平面去截一个正方体，截面不可能是（ ）
A、梯形 B、五边形 C、六边形 D、圆
13、下列立体图形中，有五个面的是（ ）
A、四棱锥 B、五棱锥 C、四棱柱 D、五棱柱
14、将一个正方体截去一个角，则其面数（ ）
A、增加 B、不变 C、减少 D、上述三种情况均有可能
15、用一个平面去截①圆锥；②圆柱；③球；④五棱柱，能得到截面是圆的图形是 ( )
A．①②④ B．①②③ C．②③④ D．①③④
16、在下列几何体中，不能展开成平面图形的是（ ）
A、棱柱 B、圆柱 C、圆锥 D、球
17、如图是用4个长方体搭成的图形，从左面看，它应是下列图形中的( )
18、如图，把一个正方形三次对折后沿虚线剪下则得到的图形是( )
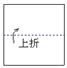
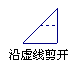
(A) (B) (C) (D)
19、平面内有5个点，每两个点都用直线连接起来，则最多可得 条直线，最少可得 条直线。
20、笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了_________;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____________.
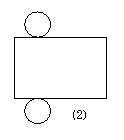
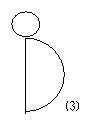
21、下图所示的三个几何体的截面分别是：
(1)_________；(2)__________；(3)___________．
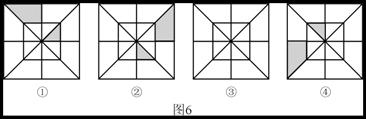
22、（2004年四川资阳）分析图6①,②,④中阴影部分的分布规律，按此规律在图6③中画出其中的阴影部分.
23、一个几何体，是由许多规格相同的小正方体堆积而成的，某主视图、左视图如图所示，要摆成这样的图形，至少需用________块正方体，最多需用_________正方体.
 |
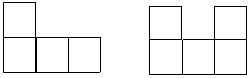24、在同一平面内用游戏棒搭4个大小一样的等边三角形，至少要________根游戏棒；在空间搭4个一样大小的等边三角形，至少要________根游戏棒.
25、如图，把第一行的图形绕虚线旋转一周，便能形成第二行的某个几何体，请用线连起来.
 |
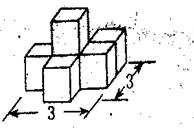
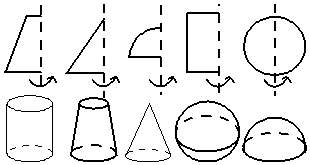26、右图的几何体由若干个棱长为1的正方体堆放而成，则这个几何体的体积为 。
27、已知三棱柱有5个面、6个顶点、9条棱，
四棱柱有6个面、8个顶点、12条棱，
五棱柱有7个面、10个顶点、15条棱，……，
由此可以推测n棱柱有_____个面，____个顶点，_____条棱。
28、依照下面图中所给图形的变化规律,
在空格中填图.
29、如图是由几个小正方体堆成的几何体，请以如图所示的正面为主视方向画出它的主视图、左视图、俯视图.
30、将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现在有一个长为4cm、宽为3cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱体，它们的体积分别是多大？
31、想一想，哪种几何体的表面展开成如下的平面图形，画出表示这些几何体的立体图形．
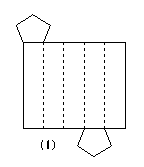
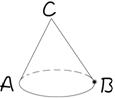
32、如图，在圆锥底面圆周B点有一只蚂蚁，要从圆锥体侧面爬一圈后，再回到B点，请你结合圆锥的展开图设计一条最短路径。
