2005年湖州市“期望杯”数学竞赛试题（初一组）
学校： 姓名： 准考证号： 成绩：
说明：本试卷满分120分；时间120分钟（12月4日上午9：00---11：00）。
一、选择题（每小题5分，共30分）：
1． 已知a,b是两个有理数, ab>a, a-b>b,对于下列三个结论：（1） a<1且b<1；
（2） ab<0；（3）a≠0且b≠0。 正确的个数是（ ）.
（Ａ） 3 （Ｂ） 2 （Ｃ） 1 （Ｄ） 0
2． 有3个数，一个是最小的奇质数，一个是小于50的的最大质数，
一个是大于60的最小质数，则这3个数的和是( )
A、101 B、110 C、111 D、113
3.已知关于
的方程
的解满足
，则
的值是（ ）.
（Ａ）10或
（Ｂ）10或
（Ｃ）－10或 （Ｄ）－10或
4.两个正数的和是60，它们的最小公倍数是273，则它们的乘积是（ ）
（A）273 （B）819 （C）1199 （D）1911
5．某轮船往返于A、B两地之间,设轮船在静水中的速度不变,那么,当水的流速增大时,
轮船往返一次所用的时间( ).
（Ａ）不变 （Ｂ）增加 （Ｃ）减少 （Ｄ）增加、减少都有可能
6．对于数x，符号[ x ]表示不大于x的最大整数例如[ 3.14 ]=3, [－7.59]= －8
则关于x的方程[
]=4的整数根有（ ）.
（Ａ）4个 （Ｂ）3个 （Ｃ）2个 （Ｄ）1个
二、填空题（每小题5分，共30分）：
1、已知
，
，
，且
＞
＞
，则
＝ ；
2、某班级共48人，春游时到湖州太湖山庄划船，每只小船坐3人，租金16元，每只大船坐5人，租金24元，则该班至少要花租金_______________元;
3、设多项式
，已知当＝0时，
；当
时，
，则当
时，
＝ ；
4、将正偶数按下表排列成5列：
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 2 | 4 | 6 | 8 | |
| 第二行 | 16 | 14 | 12 | 10 | |
| 第三行 | 18 | 20 | 22 | 24 | |
| 第四行 | 32 | 30 | 28 | 26 | |
| …… | … | … | … | … |
根据表中的规律，偶数2004应排在第 行，第 列；
5、一队卡车运一批货物，若每辆卡车装7吨货物，则尚余10吨货物装不完；若每辆卡车装8吨货物，则最后一辆卡车只装3吨货物就装完了这批货物，那么这批货物共有____吨。
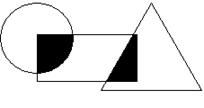6、如图圆中的阴影部分面积占圆面积的
，占长方形面积的
；三角形中阴影部分面积占三角形面积的
，占长方形面积的
. 则圆、长方形、三角形的面积比________________。
三、解答题：（每小题20分，共60分）
1. 已知：a与b互为相反数，且
，求
的值
2．某城市自来水收费实行阶梯水价，收费标准如下表所示：
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过18吨的部分 | 超过18吨的部分 |
| 收费标准（元/吨） | 2.00 | 2.50 | 3.00 |
某户5月份交水费45元，则该用户5月份的用水量是多少？
3．将分别写有数码1，2，3，4，5，6，7，8，9的九张正方形卡片排成一排，发现恰是一个能被11整除的最大的九位数，请你写出这九张卡片的排列次序列，并简述推理过程。
2005年湖州市“期望杯”七年级数学竞赛试卷
参考答案
一、选择题（每小题5分，共30分）：C C A B B B
二、填空题（每小题5分，共30分）：
1. 0或-2， 2. 232， 3. –17 4.115， 5.251,3 6. 24:20:45
三、解答题：（第1题 12分第2题12分，第3题16分）
1.
2. 解：设该用户5月份的用水量为x吨，根据题意得：
12×2+6×2.5+3（x-18）= 45
解得x=20
答：该用户5月份的用水量为20吨。
3.设九位数的奇位数字之和为x偶位数字之和为y，则x + y = 1+ 2 +3 +…… +8 + 9 = 45，且x-y=0，11，22，33或44。
∵x + y与x – y的奇偶性相同，∴x – y =11或33。
即（1）
∴由（1）得
或（2）得
（舍）
∴九位数要取到最大，
∴只有即为所求。