第五章 《相交线与平行线》测试题
学号 姓名 成绩
一、选择题（每小题3分，共30分）
 |
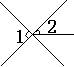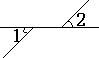
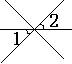
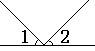1、下面四个图形中，∠1与∠2是对顶角的图形 （ ）
A、1个 B、2个 C、3个 D、4个
2、一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度是 （ ）
A、 第一次右拐50 o，第二次左拐130 o
B、 第一次左拐50 o，第二次右拐50 o
C、 第一次左拐50 o，第二次左拐130 o
D、 第一次右拐50 o，第二次右拐50 o
3、同一平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（ ）
A、a∥d B、b⊥d C、a⊥d D、b∥c
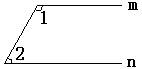4、如图，若m∥n，∠1=105 o，则∠2= （ ）
A、55 o B、60 o
C、65 o D、75 o
5、下列说法中正确的是 （ ）
A、 有且只有一条直线垂直于已知直线
B、 从直线外一点到这条直线的垂线段，叫做这点到这条直线距离
C、 互相垂直的两条线段一定相交
D、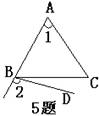 
直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3cm，则点A到直线c的距离是3cm
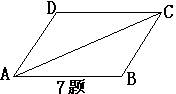
6、两条直线被第三条直线所截，下列条件中，不能判断这两人条直线平行的的是
（ ）
A、同位角相等 B、内错角相等 C、同旁内角互补 D、同旁内角相等
7、下列句子中不是命题的是 （ ）
A、两直线平行，同位角相等。 B、直线AB垂直于CD吗？
C、若︱a︱=︱b︱，则a 2 = b 2。 D、同角的补角相等。
8、下列说法正确的是 （ ）
A、 同位角互补 B、同旁内角互补，两直线平行
C、内错角相等 D、两个锐角的补角相等
9、如图，能判断直线AB∥CD的条件是 （ ）
A、∠1=∠2 B、∠3=∠4
C、∠1+∠3=180 o D、∠3+∠4=180 o
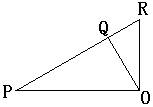
10、如图，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（ ）的长
A、PO B、RO C、OQ D、PQ
二、填空题（每空2分，共36分）
1、两个角的两边互相平行，且一个角的
等于另一个角的
，则这两个角分别是
2、下面生活中的物体的运动情况可以看成平移的是
（1）摆动的钟摆（2）在笔直的公路上行驶的汽车（3）随风摆动的旗帜（4）摇动的大绳（5）汽车玻璃上雨刷的运动（6）从楼顶自由落下的球（球不旋转）
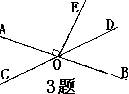
3、如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=38 o ，则∠AOC= ，∠COB= 。
4、如图，AC平分∠DAB，∠1=∠2。填空：
因为AC平分∠DAB，所以∠1= ，
所以∠2 = ，所以AB∥ 。
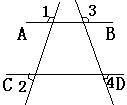
5、如图，∠1、∠2是直线 、 被第三条直线 所截成的 角。
6、把命题“对顶角相等”写成“如果……，那么……”的形式为：
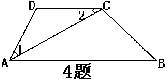
7、如图：（1）当 ∥ 时，∠DAC=∠BCA；（2）当 ∥ 时，∠ADC+∠DAB=180 o ；（3）当 = 时，AB∥DC。
三、仔细想一想，完成下面的推理过程（每空1分，共10分）
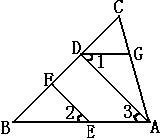
1、 如图EF∥AD，∠1=∠2，∠BAC=70 o，求∠AGD。
解：∵EF∥AD，
∴∠2= （ ）
又∵∠1=∠2，
∴∠1=∠3，
∴AB∥ （ ）
∴∠BAC+ =180 o（ ）
∵∠BAC=70 o，∴∠AGD= 。
2、 如图，已知∠BED=∠B+∠D，试说明AB与CD的关系。
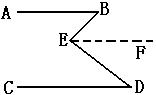解：AB∥CD，理由如下：
过点E作∠BEF=∠B
∴AB∥EF（ ）
∵∠BED=∠B+∠D
∴∠FED=∠D
∴CD∥EF（ ）
∴AB∥CD（ ）
四、画一画（每题5分，共10分）
1、如图，一辆汽车在直线形公路AB上由A向B行驶，M、N是分别位于公路AB两侧的村庄。设汽车行驶到点P时，离村庄M最近，汽车行驶到点Q时，离村庄N最近，请在图中公路AB上分别画出点P、Q的位置。
2、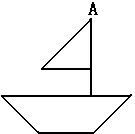
把下图中的小船向右平移，使得小船上的点A向右平移5cm到A′。
五、解答题（每小题分，共分）
1、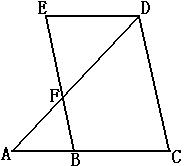
如图，EB∥DC，∠C=∠E，请你说出∠A=∠ADE的理由。
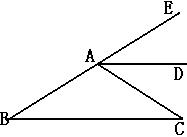2、如图，AD是∠EAC的平分线，AD∥BC，∠B=30 o，求∠EAD、∠DAC、∠C的度数。