第四章《代数式》测试卷
班级 学号 姓名
一.填空题。(每题3分,共24分)
1.实数![]()
![]() 的相反数的倒数是 。
的相反数的倒数是 。
2.一个负数的绝对值等于它的相反数,若这个负数用字母![]() 表示,则这条数学规律可表示成
。
表示,则这条数学规律可表示成
。
3.单项式![]() 的系数是
,次数是 。
的系数是
,次数是 。
4.多项式![]() 的最高次项是
,最高次项的系数是 。
的最高次项是
,最高次项的系数是 。
5.一年期的存款的年利率为![]() ,利息个人所得税的税率为20%。某人存入的本金为
,利息个人所得税的税率为20%。某人存入的本金为![]() 元,则到期支出时实得本利和为 元。
元,则到期支出时实得本利和为 元。
6.植树节,小明种树棵数比小聪多![]() ,则小聪种树的棵数比小明少 %。
,则小聪种树的棵数比小明少 %。
7.已知多项式![]() ,当
,当![]() 时,多项式的值为17。则该多项式当
时,多项式的值为17。则该多项式当![]() 时的值是
。
时的值是
。
8.已知甲、乙两种糖果的单价分别是![]() 元/千克和12元/千克。为了使甲乙两种糖果分别销售与把它们混合成什锦糖后再销售收入保持不变,则由20千克甲种糖果和
元/千克和12元/千克。为了使甲乙两种糖果分别销售与把它们混合成什锦糖后再销售收入保持不变,则由20千克甲种糖果和![]() 千克乙种糖果混合而成的什锦糖的单价应是
元/千克。
千克乙种糖果混合而成的什锦糖的单价应是
元/千克。
二.选择题(每题3分,共18分)
( )9。下列说法正确的是:(A)![]() 是负数 (B)
是负数 (B)![]() 一定是非负数
一定是非负数
(C)不论![]() 为什么数,
为什么数,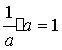 (D)
(D)![]() 一定是分数
一定是分数
( )10。已知![]() 是两位数,
是两位数,![]() 是一位数,把
是一位数,把![]() 接写在
接写在![]() 的后面,就成为一个三位数。这个三位数可表示成:
的后面,就成为一个三位数。这个三位数可表示成:
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
( )11。一个代数式的2倍与![]() 的和是
的和是![]() ,这个代数式是:
,这个代数式是:
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
( )12。在下列代数式中:![]()
![]()
![]() 其中值永远等于0的有:
其中值永远等于0的有:
(A)4个 (B)3个 (C)2个 (D)1个
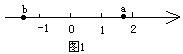 ( )13。已知
( )13。已知![]() 两数在数轴上的表示如图1所示,那么化简代数式
两数在数轴上的表示如图1所示,那么化简代数式![]() 的结果是:
的结果是:
(A)1 (B)![]()
(C)![]() (D)—1
(D)—1
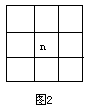 ( )14。在排成每行七天的日历表中取下一个
( )14。在排成每行七天的日历表中取下一个![]() 方块(如
方块(如
图2)。若所有日期数之和为189,则n的值为:
(A)21 (B)11 (C)15 (D)9
三.解答题。(共58分)
15.(10分)化简并求值。
![]() ,其中
,其中![]()
![]() ,其中
,其中![]()
 16.(6分)同一时刻的北京时间、巴黎时间、东京时间如图所示。
16.(6分)同一时刻的北京时间、巴黎时间、东京时间如图所示。
(1) 设北京时间为![]() 分别用代数式表示同一时刻巴黎时间和东京时间;
分别用代数式表示同一时刻巴黎时间和东京时间;
(2) 2001年7月13日北京时间22:08,国际奥委会主席萨马兰奇宣布,北京获得2008年第29届夏季奥运会的主办权。问这一时刻巴黎时间、东京时间分别为几时?
17.(8分)1千瓦时电(即通常所说的1度电)可供一盏40瓦的电灯点亮25小时。
(1) 1千瓦时的电量可供n瓦的电灯点亮多少时间?
(2) 若每度电的电费为a元,一个100瓦的电灯使用12时的电费是几元?
18、(9分)四人做传数游戏,甲任报一个数给乙,乙把这个数加1传给丙,丙再把所得的数平方后传给丁,丁把所听到的数减1报出答案:(7分)
1、 如果甲所报的数为x,请把丁最后所报的答案用代数式表示出来。
2、 若甲报的数为9,则丁的答案是多少?
3、 若丁报出的答案是15,则甲传给乙的数是多少?
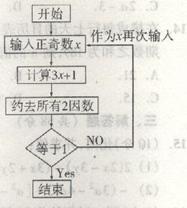
19(8分)利用计算器,按如图流程图操作:
(1) 若首次输入的正奇数为11,则按流程图操作的变化过程,可表示为:11→17→13→5→1。请用类似的方法分别表示首次输入的正奇数为9,19时,按流程图操作的变化过程;
(2) 根据你的操作结果,给出一个猜想,并清楚地叙述你的猜想
20、某市出租车收费标准是:起步价10元,3千米后每千米1.20元, (7分)
1、 若某人乘坐了x(x>3)千米的路程,则他应支付的费用是多少?
2、 若他支付了16元车费,你能算出他乘坐的路程吗?
21.(10分)任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的二位数(有6个)。求出所有这些二位数的和,然后将它除以原三位数的各个数位上的数之和。例如,对三位数223,取其两个数字组成所有可能的二位数:22,23,22,23,32,32。它们的和是154。三位数223各位数的和是7,![]() 。再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果正确。
。再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果正确。
答案
1)![]() 。2)
。2)![]() ,3)
,3)![]() ,2次,4)
,2次,4)![]() ,5)
,5)![]() ,
,
6)![]() ,7)1,8)
,7)1,8)![]() ,9B 10C 11D 12C 13B 14A
,9B 10C 11D 12C 13B 14A
15)(1)![]() (2)
(2)![]()
16)(1)巴黎:![]() 东京:
东京:![]() (2)巴黎:15:08 东京:23:08
(2)巴黎:15:08 东京:23:08
17)(1)![]() 时,(2)
时,(2)![]() 元。 18)(1)0.23198x美元(2)2965.6美元
元。 18)(1)0.23198x美元(2)2965.6美元
19)(1)9→7→11→17→13→5→1;19→29→11→17→13→5→1(2)略
(3)任何正奇数按流程图操作,最终变成1
20,举例1三位数:578:![]()
举例2:三位数123:![]()
结论:商为定值22.说明:设三位数为![]() ,则
,则![]()
![]() .
.