七年级数学第三章测试卷
(时间:90分钟 总分:100分)
一、填空题:(每空1.5分,共45分)
1.82°32′5″+______=180°.
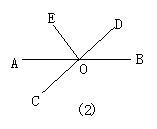
2.如图1,线段AD上有两点B、C,图中共有______条线段.
3.一个角是它补角的一半,则这个角的余角是_________.
4.线段AB=5cm,C是直线AB上的一点,BC=8cm,则AC=________.
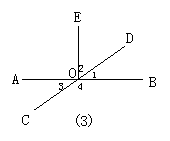
5.如图2,直线AB、CD相交于点O,OE平分∠COD,则∠BOD的余角______, ∠COE的补角是_______,∠AOC的补角是______________________.
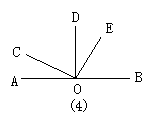
6.如图3,直线AB、CD相交于点O,∠AOE=90°,从给出的A、B、
C三个答案中选择适当答案填空.
(1)∠1与∠2的关系是( )
(2)∠3与∠4的关系是( )
(3)∠3与∠2的关系是( )
(4)∠2与∠4的关系是( )
A.互为补角 B.互为余角 C.即不互补又不互余
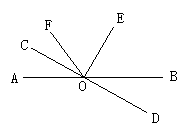
7.如图4,∠AOD=90°,∠COE=90°,则图中相等的锐角有_____对.
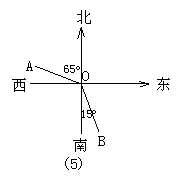
8.如图5所示,射线OA表示_____________方向,射线OB表示______________方向.
9.四条直线两两相交时,交点个数最多有_______个.
10.如果一个角是30°,用10倍的望远镜观察,这个角应是_______°.
11.38°41′的角的余角等于________,123°59′的角的补角等于________.
12.如果∠1的补角是∠2,且∠1>∠2,那么∠2的余角是________(用含∠1 的式子表示).
13.如果∠α与∠β互补,且∠α:∠β=5:4,那么,∠α=_______,∠β=_________.
14.根据下列多面体的平面展开图,填写多面体的名称.
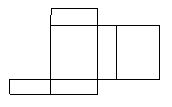
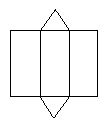
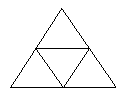
(1)__________,(2)__________,(3)_________.
15.指出图(1)、 图(2) 、图(3)是左边几何体从哪个方向看到的图形。
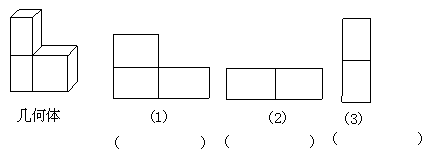
16.圆锥由_______面组成,其中一个是_______面 ,另一个是_______面.
二、选择题:(每题3分,共15分)
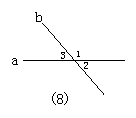
17.如图8,直线a、b相交,∠1=130°,则∠2+∠3=( )
A.50° B.100° C.130° C.180°
18.轮船航行到C处观测小岛A的方向是北偏西48°,那么从A同时观测轮船在C处的方向是( ) A.南偏东48° B.东偏北48° C.东偏南48° D.南偏东42°
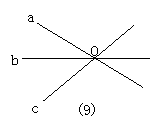
19.如图9,三条直线相交于O点,则图中相等的角(平角除外)有( )对
A.3对 B.4对 C.6对 D.8对
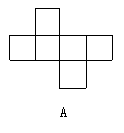
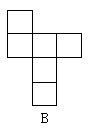
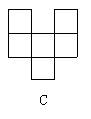
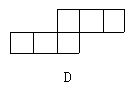
20.下列图形不是正方体展开图的是( )
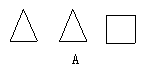
21.从正面、上面、左面看四棱锥，得到的3个图形是( )
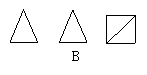
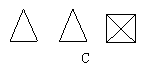
计算题:(每题10分,共30分)
32. 如图,已知C是AB的中点,D是AC的中点,E是BC的中点.
(1)若AB=18cm,求DE的长;(2)若CE=5cm,求DB的长.
33.如图3-12,已知直线AB和CD相交于O点,∠COE是直角,OF 平分∠AOE, ∠COF=34°,求∠BOD的度数.
34.一个角的余角比它的补角的
还少20°,求这个角.
六:(10分)
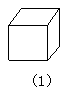
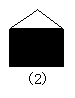
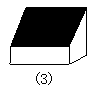
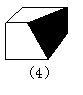
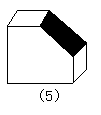
36.如图,图(1)是正方体木块,把它切去一块,可能得到(2)、(3)、(4)、 (5)所示的图形,问(2)、(3)、(4)、(5)图中切掉的部分可能是其他几块中的哪一块?
39.如图,A、B两地隔着湖水,从C地测得CA=50m,CB=60m,∠ACB=145°,用1 厘米代表10米(就是1:1000的比例尺)画出如图的图形.量出AB的长(精确到1毫米), 再换算出A、B间的实际距离.
答案:
一、
1.97°27′55″ 2.6 3.30° 4.13cm或3cm 5.∠AOE ∠DOE ∠AOD 与∠BOC
6.(1)B (2)A (3)B (4)C
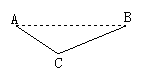
7.审题及解题迷惑点:由∠BAC=90°,可得到∠B与∠C互余,由同角的余角相等,在此须在图中再找出∠B的余角便可找出与∠C相等的角,同样若再找出与∠C 互为余角的角便是与∠B相等的角.
解:如答图所示.
∵∠BAC=90°,∴∠B+∠C=90°.
又∵∠ADC=90°,∴∠DAC+∠C=90°.
∴∠B=∠DAC.
同理可得∠C=∠DAB.
8.北偏西65°或西偏北25°方向;南偏东15°或东偏南75°方向.
9.6 10.30°
11.51°19′ 56°1′. 12. 
或∠1-90°
13.100° 80° 14.(1)长方体 (2)三棱柱 (3)三棱锥 15.(1)正视图 (2)俯视图 (3)左视图 16. 两个;曲面;平面
二、17.B 18.A 19.C
20.审题及解题迷惑点:首先认真观察图形,充分运用空间想像能力,分析思考这四个图形中的哪些图形能还原成原几何图形,哪个图不能.
21.C
三、22.× 23.∨ 24.∨ 25.∨ 26.× 27.× 28.× 29.× 30. ∨ 31.×
四、
32. (1)∵C是AB的中点,
∴AC=BC=
AB=9(cm).
∵D是AC的中点,
∴AD=DC=AC=
(cm).
∵E是BC的中点,
∴CE=BE=BC=(cm)
又∵DE=DC+CE,
∴DE=+=9(cm).
(2)由(1)知AD=DC=CE=BE,
∴CE=BD.
∵CE=5cm,
∴BD=15(cm)
33.解:如答图,∵∠COE=90°,∠COF=34°,
∴∠EOF=90°-34°=56°.
∵OF平分∠AOE,
∴∠AOE=∠EOF=56°.
∴∠AOC=∠AOF-∠COF=56°-34°=22°.
∵∠AOC=∠BOD(对顶角相等),
∴∠BOD=22°.
34.解:设这个角为α,则这个角的余角为90°-α,补角为180°-α,
依题意,得 
,解得α=75°.
答:这个角为75°.
35.解:设这个角为α,则余角为90°-α,由题意,得
α=180°-123°24′16″=56°35′44″,
∴90°-α=90°-56°35′44″=33°24′16″.
答:这个角的余角是33°24′16″.
五、
36.审题及解题迷惑点:要作一角等于3∠1-∠2,就须先以O为顶点,以OA 为一边作∠AOD=3∠1,然后在∠AOD的内部以∠AOD的一边为边作一个角等于∠2即可.
解:
(1)以∠1的顶点O为圆心,以适当的长为半径画弧,分别交射线OA、OB于点E、F
(2)在弧上依次截取
,并使
.
(3)自O点过H点作射线OD,则∠AOD即为3∠1.
(4)以∠2的顶点为圆心,适当长为半径画弧交∠2的两边于M′、N′两点.
(5)以O为圆心,以同样长为半径画弧交OA于点M.
(6)以M为圆心,以M′N′为半径画弧交前弧于点N.
(7)自O点为N点作射线OC.
∠COD即为所求.
37.解:用三角板中的45°的角和30°的角,让其顶点和一边重合在一起,可以画出75°的角,同样的道理,用三角板中的60°的角和45 °的角可以画出105°的角.
六、
38.解:(2)图切掉的部分可能是(3)图和(5)图,(3)图切掉的部分可能是(2)图,(5)图切掉的部分可能是(2)图.
39.略.