相交线与平行线
(时间:45分钟 满分:100分) 姓名
一、选择题(每小题4分,共24分)
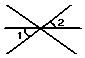
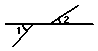
1.下面四个图形中,∠1与∠2是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
![]()
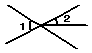
2.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130°。
B.第一次左拐50°,第二次右拐50°。
C.第一次左拐50°,第二次左拐130°。
D.第一次右拐50°,第二次右拐50°。
3.同一平面内的四条直线满足a⊥b,b⊥c,c⊥d,则下列式子成立的是( )
A.a∥b B.b⊥d
C.a⊥d D.b∥c
4.三条直线两两相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( )
A.m = n B.m>n
C.m<n D.m + n = 10
5.如图,若m∥n,∠1 = 105°,则∠2 =( )
A.55° B.60° C.65° D.75°
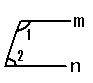
6.下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线。
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
C.互相垂直的两条直线一定相交。
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线c的距离是3cm。
二、填空题(每小题4分,共20分)
7.两个角的两边两两互相平行,且一个角的![]() 等于另一个角的
等于另一个角的![]() ,则这两个角的度数分别为
。
,则这两个角的度数分别为
。
8.猜谜语(打本章两个几何名称)。
剩下十分钱 ;两牛相斗 。
9.下面生活中的物体的运动情况可以看成平移的是 。
(1)摆动的钟摆。 (2)在笔直的公路上行驶的汽车。 (3)随风摆动的旗帜。 (4)摇动的大绳。 (5)汽车玻璃上雨刷的运动。 (6)从楼顶自由落下的球(球不旋转)。
10.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD = 38°,则∠AOC = ,∠COB = 。
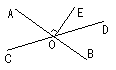
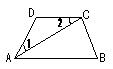
(第10题图) (第11题图)
11.如图,AC平分∠DAB,∠1 =∠2。填空:因为AC平分∠DAB,所以∠1 = 。所以∠2 = 。所以AB∥ 。
三、做一做(本题10分)
12.已知三角形ABC、点D,过点D作三角形ABC平移后的图形。
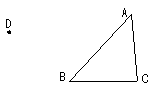
四、算一算(本题10分)
13.如图,AD是∠EAC的平分线,AD∥BC,∠B = 30°,你能算出∠EAD、∠DAC、∠C的度数吗?
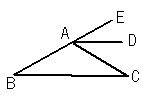
五、想一想(每空3分,共12分)
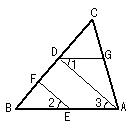
14.如图,EF∥AD,∠1 =∠2,∠BAC = 70°。将求∠AGD的过程填写完整。
因为EF∥AD,所以 ∠2 = 。又因为 ∠1 = ∠2,所以 ∠1 = ∠3。 所以AB∥ 。所以∠BAC + = 180°。又因为∠BAC = 70°,所以∠AGD = 。
六、实际应用:(本大题两小题,共24分)
15.结合本班实际,画出班级的简易平面图形,找出其中的垂线和平行线。(本题11分)
16.如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外。如何测量(运用本章知识)?(本题13分)

附:命题意图及参考答案
(一)命题意图
一、 选择题
1.考查学生对对顶角概念的理解,加深学生对平面图形的认识和感受。
2.考查学生对平行线的条件的理解及形象思维的能力。
3. 考查学生对数学知识的理解和思维的深刻性。
4.考查学生对对顶角概念的深刻理解及思维的灵活性。
5.考查学生对平行线性质掌握情况。
6.考查学生对垂直知识的掌握情况,提高学生运用基础知识解决问题的能力。
二、 填空题
7.考查学生的计算能力。
8.本题通过猜谜引发学生对有关数学概念的思考。
9.本题让学生认识平移在现实生活中的应用。
10.本题考查学生的计算能力。
11.本题意在教会学生使用数学语言有条理地表达思考的过程。
三、做一做
12.考查学生对平移作图的掌握情况,提高学生动手动脑能力。
四、算一算
13.本题意在引导学生体会数学知识之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解题能力。
五、想一想
14.本题考查学生对平行线的性质和特征的应用及它们之间的区别,使学生获得一些研究问题的方法和经验,发展思维能力。
六、实际应用
本题意在提高学生应用数学的意识,体会数学的价值。
设置探索题与开发题,可以暴露学生的思维过程,能深化学生的思维品质,发展学生的逻辑思维和创造性思维能力。
(二)参考答案
1.B
2.B
3.C
4.A
5.D
6.D
7. 72°,108°
8.余角,对顶角
9.(2)和(6)
10.52°,128°
11.∠BAC,∠BAC,CD。
12.略
13.30°,30°,30°
14.∠3,DG,∠AGD,110°
15.略
16.延长AO与BO,测∠AOB的对顶角。