第五章 相交线与平行线单元测试题
姓名：___________ 时间：90分钟 满分：100分 评分：_________
一、选择题（本大题共12小题，每小题3分，共36分．在每小题所给出的四个选项中，只有一项是符合题目要求的）
1．下列说法中，正确的是（ ）
A．一条射线把一个角分成两个角，这条射线叫做这个角的平分线;
B．P是直线L外一点，A、B、C分别是L上的三点，已知PA=1，PB=2，PC=3，则点P到L的距离一定是1;
C．相等的角是对顶角;
D．钝角的补角一定是锐角.
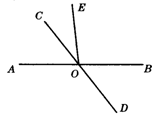
2．如图1，直线AB、CD相交于点O，过点O作射线OE，则图中的邻补角一共有（ ）
A．3对 B．4对 C．5对 D．6对
(1) (2) (3)
3．若∠1与∠2的关系为内错角，∠1=40°，则∠2等于（ ）
A．40° B．140° C．40°或140° D．不确定
4．如图，哪一个选项的右边图形可由左边图形平移得到（ ）
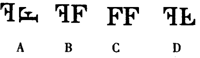
5．a，b，c为平面内不同的三条直线，若要a∥b，条件不符合的是（ ）
A．a∥b，b∥c; B．a⊥b，b⊥c;
C．a⊥c，b∥c; D．c截a，b所得的内错角的邻补角相等
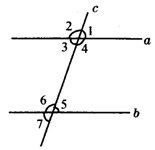
6．如图2，直线a、b被直线c所截，现给出下列四个条件：（1）∠1=∠5；（2）∠1=∠7；（3）∠2+∠3=180°；（4）∠4=∠7，其中能判定a∥b的条件的序号是（ ）
A．（1）、（2） B．（1）、（3） C．（1）、（4） D．（3）、（4）
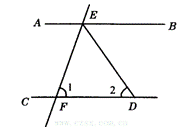
7．如图3，若AB∥CD，则图中相等的内错角是（ ）
A．∠1与∠5，∠2与∠6; B．∠3与∠7，∠4与∠8;
C．∠2与∠6，∠3与∠7; D．∠1与∠5，∠4与∠8
8．如图4，AB∥CD，直线EF分别交AB、CD于点E、F，ED平分∠BEF．若∠1=72°，则∠2的度数为（ ）
A．36° B．54° C．45° D．68°
(4) (5) (6)
9．已知线段AB的长为10cm，点A、B到直线L的距离分别为6cm和4cm，则符合条件的直线L的条数为（ ）
A．1 B．2 C．3 D．4
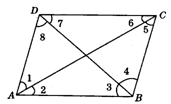
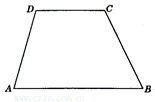
10．如图5，四边形ABCD中，∠B=65°，∠C=115°，∠D=100°，则∠A的度数为（ ）
A．65° B．80° C．100° D．115°
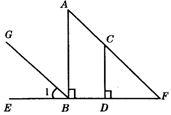
11．如图6，AB⊥EF，CD⊥EF，∠1=∠F=45°，那么与∠FCD相等的角有（ ）
A．1个 B．2个 C．3个 D．4个
12．若∠A和∠B的两边分别平行，且∠A比∠B的2倍少30°，则∠B的度数为（ ）
A．30° B．70° C．30°或70° D．100°
二、填空题（本大题共8小题，每小题3分，共24分．把答案填在题中横线上）
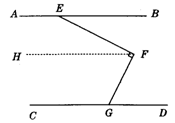
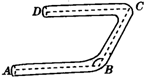
13．如图，一个合格的弯形管道，经过两次拐弯后保持平行（即AB∥DC）．如果∠C=60°，那么∠B的度数是________．
14．已知，如图，∠1=∠ABC=∠ADC，∠3=∠5，∠2=∠4，∠ABC+∠BCD=180°．将下列推理过程补充完整：
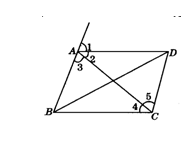（1）∵∠1=∠ABC（已知），
∴AD∥______
（2）∵∠3=∠5（已知），
∴AB∥______,
（_______________________________）
（3）∵∠ABC+∠BCD=180°（已知），
∴_______∥________,
（________________________________）
15．阅读下列语句：
（1）响应党的号召，开发大西北!
（2）“法轮功”是邪教．
（3）台湾是中华人民共和国不可分割的邻土．
（4）若ab=0，则a=0．
（5）两直线平行，同旁内角互补．
在上述语句中，属于正确命题的是第________句（填入句子的序号）．
16．已知直线AB、CD相交于点O，∠AOC-∠BOC=50°，则∠AOC=_____度，∠BOC=___度．
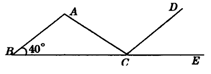
17．如图7，已知B、C、E在同一直线上，且CD∥AB，若∠A=105°，∠B=40°，则∠ACE为_________．
(7) (8) (9)
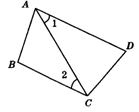
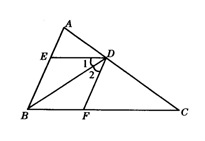18．如图8，已知∠1=∠2，∠D=78°，则∠BCD=______度．
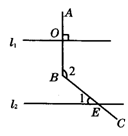
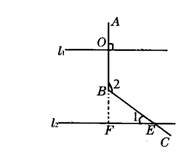
19．如图9，直线L1∥L2，AB⊥L1，垂足为O，BC与L2相交于点E，若∠1=43°，则∠2=_______度．
20．如图，∠ABD=∠CBD，DF∥AB，DE∥BC，则∠1与∠2的大小关系是________．
三、解答题（本大题共6小题，共40分，解答应写出文字说明，证明过程或演算步骤）
21．（6分）已知∠BOC与∠AOB互为邻补角，又OD、OE分别是∠AOB、∠BOC的平分线，若∠AOB=80°，求∠DOE的度数．
22．（7分）如图，AB∥A′B′，BC∥B′C′，BC交A′B′于点D，∠B与∠B′有什么关系？为什么？
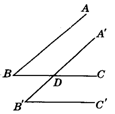
23．（6分）如图，已知AB∥CD，试再添上一个条件，使∠1=∠2成立（要求给出两个答案）．
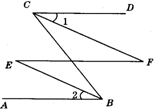
24．（6分）如图，AB∥CD，∠1：∠2：∠3=1：2：3，说明BA平分∠EBF的道理．
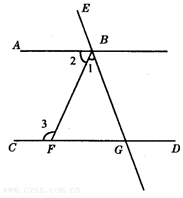
25．（7分）如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1=∠2，∠3=80°．求∠BCA的度数．
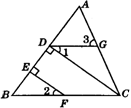
26．（8分）如图，EF⊥GF于F．∠AEF=150°，∠DGF=60°，试判断AB和CD的位置关系，并说明理由．
答案:
1．D
2．D 点拨：图中的邻补角分别是：∠AOC与∠BOC，∠AOC与∠AOD，∠COE与∠DOE，∠BOE与∠AOE，∠BOD与∠BOC，∠AOD与∠BOD，共6对，故选D．
3．D 4．C 5．C 6．A
7．C 点拨：本题的题设是AB∥CD，解答过程中不能误用AD∥BC这个条件．
8．B 点拨：∵AB∥CD，∠1=72°，
∴∠BEF=180°-∠1=108°．
∵ED平分∠BEF，
∴∠BED=
∠BEF=54°．
∵AB∥CD，∴∠2=∠BED=54°．故选B．
9．C 点拨：如答图，L1，L2两种情况容易考虑到，但受习惯性思维的影响，L3这种情况容易被忽略．
10．B
11．D 点拨：∠FCD=∠F=∠A=∠1=∠ABG=45°．
故选D．
12．C 点拨：由题意，知
或
解之得∠B=30°或70°．故选C．
13．120°
14．（1）BC；同位角相等，两直线平行
（2）CD；内错角相等，两直线平行
（3）AB；CD；同旁内角互补，两直线平行
15．（2），（3），（5）
16．115；65
点拨：设∠BOC=x°，则∠AOC=x°+50°．
∵∠AOC+∠BOC=180°．
∴x+50+x=180，解得x=65．
∴∠AOC=115°，∠BOC=65°．
17．145°
18．102
19．133
点拨：如答图，延长AB交L2于点F．
∵L1∥L2，AB⊥L1，∴∠BFE=90°．
∴∠FBE=90°-∠1=90°-43°=47°．
∴∠2=180°-∠FBE=133°．
20．∠1=∠2
21．解：如答图，由邻补角的定义知∠BOC=100°．
∵OD，OE分别是∠AOB，∠BOC的平分线，
∴∠DOB=∠AOB=40°，∠BOE=∠BOC=50°．
∴∠DOE=∠DOB+∠BOE=40°+50°=90°．
22．解：相等
理由 ∵AB∥A′B′，BC∥B′C′，
∴∠B=∠A′DC，∠A′DC=∠B′，
∴∠B=∠B′．
23．CF∥BE或CF、BE分别为∠BCD、∠CBA的平分线等．
24．解：设∠1、∠2、∠3分别为x°、2x°、3x°．
∵AB∥CD．
∴由同旁内角互补，得2x+3x=180，解得x=36．
∴∠1=36°，∠2=72°．
∵∠EBG=180°，
∴∠EBA=180°-（∠1+∠2）=72°．
∴∠2=∠EBA．
∴BA平分∠EBF．
25．解：CD⊥AB，FE⊥AB，∴CD∥EF，∴∠2=∠FCD．
∵∠1=∠2，∴∠1=∠FCD．
∴DG∥BC．∴∠BCA=∠3=80°．
26．解：AB∥CD．
理由：如答图，过点F作FH∥AB，则∠AEF+∠EFH=180°．
∵∠AEF=150°，∴∠EFH=30°．
又∵EF⊥GF，∴∠HFG=90°-30°=60°．
又∵∠DGF=60°，
∴∠HFG=∠DGF．
∴HF∥CD，从而可得AB∥CD．
