七年级第四、五章数学测试题
一、细心的选一选（本大题12个小题，每小题4分，共48分）
1、关于x的方程2(x – 1) – a =0的根是3，则a的值是（ ）
A．4 B．- 4 C．5 D．- 5
2、下列说法错误的是（ ）
A．3x – 2x =5x是方程 B．x = 0是方程 C．2x – 3y=1是方程 D．π=3.14是方程
3、方程2x – 1 =0的解是（ ）
A．x = 2 B．x = 1 C．x =－
D．x =
4、若
是一元一次方程，则m的值为（ ）
A．m=1 B.m=-1 C.m=2 D.m=-2
5、解方程
时，去分母后得到的方程是（ ）
A．2(2x – 1) – 1 + 3x = -4 B．2(2x – 1) – 1 + 3x = - 1
C．2(2x – 1) – 1 – 3x = - 16 D．2(2x – 1) – (1 + 3x) = -4
6、若2amb2m+3n与amb8的和仍是一个单项式，则m与n的值分别是（ ）
A．1，2 B．2，1 C．1，1 D．1，3
7、有一种足球是由32块黑白相间的牛皮缝制而成的（如下图），黑皮可看作正五边形，白皮可看作正六边形．设白皮有x块，则黑皮有(32 - x)块，每块白皮有六条边，共6x条边，因每块白皮有三条边和黑皮连在一起，故黑皮共有3x条边．要求出白皮、黑皮的块数，列出的方程正确的是(
)
A．3x=32 - x B．3x=5(32- x) C．5x=3(32 - x) D．6x=32- x
8、某种出租车的收费标准是：起步价7元（即行驶距离不超过3千米都需付7元车费），超过3千米以后，每增加1千米，加收2.4元（不足1千米按1千米计），某人乘这种出租车从甲地到乙地共支付车费19元，设此人从甲地到乙地经过的路程是x千米，那么x的最大值是（ ）
A．11 B．8 C．7 D．5
10、当代数式a+b的值为3时，代数式2a+2b+1的值是（ ）
A．5 B．6 C．7 D．8
11、在时刻8：30，时钟上的时针和分针之间的夹角为（ ）
A．85° B．75° C．70° D．60°
12、已知同一平面内的直线L1、L2、L3，如果L1⊥L2，L2L3，那么L1与L3的位置关系是（ ）
A．平行 B．相交 C．垂直 D．以上全不对
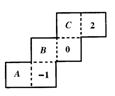13、如图是一个正方体的表面展开图，若在其中的三个正方形A、B、C内分别填上适当的数，使得将这个表面展开图沿虚线折成正方体后，相对面上的两数互为相反数，则填在4、曰、C内的三个数依次是( )
A．0，-2，1 B．0，l，-2 C．1，0，-2 D．-2，O，1
二、耐心的填一填（本大题12个小题，每小题3分，共36分
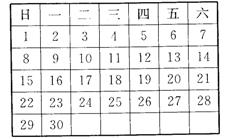
1、在2003年6月的日历（如下图）中，任意图出一竖列上相邻的三个数，设中间的一个数为x，则其余两个数分别为 。
 |
2、右上图是一幅“苹果图”，第一行有1个苹果，第二行有2个，第三行有4个，第四行有8， ……。你是否发现苹果的排列规律？猜猜看，第十行有 个苹果。
3、观察下列各式：
，
×3=+3，
×4=+4，
×5=+5……
想一想，什么样的两数之积等于两数之和？设n表示正整数，用关于n的等式表示这个规律为： × = + 。
4、如果x – 3=0，那么x=
5、有一大捆粗细均匀的电线，现要确定其长度，从中先取出1米长的电线，称出它的质量为a，再称出其余电线的总质量为b，则这捆电线的总长度是 。
6、当x
= 时，代数式
(1 – 2x)与代数式
(3x + 1)的值相等。
7、若关于x的方程6x + 3m = 22与5x – 6 =4的解相同，则m的值为 。
8、a、b、c、d为实数，现规定一种新的运算：
=ad – bc，那么当
=18时，x= 。
9、已知线段AB，延长AB到C，使BC=AB，D为AC的中点，若DC=4cm，则AB的
长是
10、如果x – 2+(x – y +3)2=0，那么(x – y)2 。
三、认真的解一解（本大题8个小题，共66分）
1、先化简，再求值：
2、阅读理解题（7分）
（1）阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为AB。
当A、B两点中有一点在原点时，不妨设点A在原点，如图1 – 1 –7（1），AB=OB =b=a – b；当A、B两点都不在原点时，
①如图1 – 1 –7（2），点A、B都在原点的右边，AB=OB - OA=b - a=b – a=a – b；
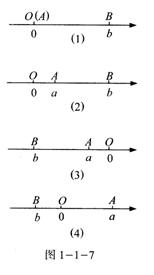②如图1 – 1 –7（3），点A、B都在原点的左边，AB=OB - OA=b - a=-b-(-a)=a – b；
③如图1 – 1 –7（4），点A、B都在原点的两边，AB=OA + OB=a + b=a+(-b)= a – b。
综上，数轴上A、B两点之间的距离AB=a – b。
（2）回答下列问题：
①数轴上表示2和5的两点之间的距离是 ，数轴上表示-2和-5的两点之间的距离是 ，数轴上表示1和-3的两点之间的距离是 ；
②数轴上表示x和-1的两点A和B之间的距离是 ，如果AB=2，那么x为 ；
③当代数式x+1+x – 2取最小值时，相应的x的取值范围是 。
3、解方程（每小题4分，共12分）
(1)
(3) 
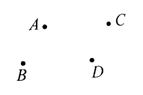4、（6分）如右图，平原上有A、B、C、D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池，不考虑其他因素，请你画图确定蓄水池H点的位置，使它与四个村庄的距离之和最小，并用文字说明理由。
5、（7分）根据下图给出的信息，求每件T恤衫和每瓶矿泉水的价格。
 |
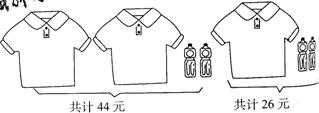6、(8分)某商场出售某种文具，每件可盈利2元，为了支援贫困山区，现在按原售价的7折出售给一山区学校，结果每件盈利0.2元（盈利=售价 – 进货价），问该文具每件的进货价是多少元？
31、（8分）王大伯承包了25亩土地，今年春季改种茄子和西红柿两种大棚蔬菜，用去了44000元，其中种茄子每亩用了1700元，获纯利2400元；种西红柿每亩用了1800元，获纯利2600元，问王大伯一共获纯利多少元？
7、(10分)某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元。
（1）求该同学看中的随身听和书包的单价各是多少元？
（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一定超市购买看中的这两样物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？