七年级（下）数学期末复习试卷（北师大版）
班级 学号 姓名 成绩
.一。填空（每小题2分，共20分）
1。数轴上与—2这个点的距离为3的点所表示的数是（ ）。
2。单项 式—4xy的次数是（ ）。
3。∠α的余角的三分之二为36°，∠α的余角为（ ）°。
4。把—0。保留四个有效数字并写成科学记数法得（ ）。
5。布袋里有除颜色外都相同的3个红球、2个黄球，现从中摸出两个球，则两个都是红球的概率为
（ ）。
6。如图（1）AD∥BC，要使△ABC ≌△CDA,则仅需添加的一个条件是（
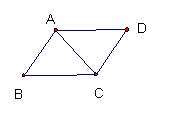
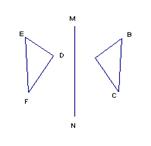
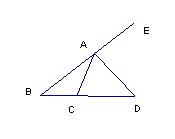
图1 图2 图3
）。
7。某地固定电话的收费方式不为：前3分钟（不足3分钟按3分钟算）收0。2元，以后每增加1分钟（不足1分钟按1分钟算）加收0。1元，则通话费Y（元）与通话时间X（分钟）之间的关系为（
）。
8。如图（2），△ABC与△DEF关于直线MN对称，若AB=2a,BC=3a,DF=
x,则x 的取值范围是（
）。
9。若（a+b）
=5x，(a-b) =x,则ab=( )。
10。时钟在6点过（ ）分时，时针与分针的夹角为114°。
二。选择题（共30分，每小题3分）。
11。下列结论，正确的个数为（ ）。
〈1〉单项式
的次数是2。〈2〉a
=1。〈3〉（— 
）×2÷ =4。〈4〉（-m-1) =m +2m+1。〈5〉有斜边和一个锐角对应相等的两个直角三角形全等。
〈6〉（a
）
=(a) 。
A，1。 B，2。 C，3。 D，4。
12。如图（3）在△ABC中，∠ABC=35°，AD 平分∠CAE，∠DAE=60°，则∠ACD=[ ]。
A，25°。 B，85°。 C，60°。 D，95°。
13。x是最大的负整数，则多项式X
+X的值为（其中n的值为正整数）[
]。
A，—2。 B，2。 C，0。 D，1。
14。若∠1+∠2=90°，∠2与∠3互余，则∠1与∠3的关系为[ ]。
A，相等。 B，互余。 C，互补。 D，不确定。
15。光的速度为3×10
米/秒，能达到光速百万分之一的是[ ]。
A，自行车。 B，飞机。 C，火车。 D，汽车
16。甲说：“我县今年10月1日会下雨。”乙反驳道：“我县今年10月1日不会下雨。”那么，两人说法实现的概率分别为[ ]。
A，0、0。 B， ，1。
C，1， 1。 D， ， 。
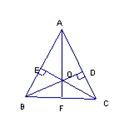
图4
17。如图（4），在△ABC中 ，AB=AC，BD⊥AC于D，CE⊥AB于E，则图中 全等的直角三角形有[ ]对。
A，5。 B，6。 C，4。 D，3。
18。若8×2
=5
，当y= - 9时，x应等于[ ]。
A，- 3。 B，- 4。 C，0。 D，2。
9。a、b为有理数，现规定一种运算：“a△b=（a+b）
（a—b）”则（—2）△（—3）=[
]。
A，6。 B，—5。 C，0。 D，2。
20。一个角的余角与补角也互为补角，则这个角是[ ]的角。
A，60°。 B，30°。 C，45°。 D，90°。
三。解答题（共50分，第21、22、23、24题每题5分，其余各题均为6分）。
21。化简：（2x—3）（x—2）—2（x—1）
22。若a、b互为相反数，且a、b均不
为0，化简：（a+b）—
+（
）
23。求代数式的值：[（x+y）（x—y）—（x—y）]÷2y（其中x= ，y= - 
）
24。计算：（—2b—a+c)（—a+2b—c）
。
25。甲乙二人从山脚登上山顶，下图中的两条线段分别代表甲乙二人离开山脚的距离y（米）与所用时间x（分）的关系。观察图形回答：〈1〉谁先出发？先登山多少米？〈2〉山高多少米？谁先登上山顶
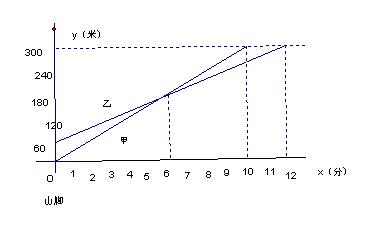
26。如图，AD⊥BC，垂足为D，DE∥AB，∠B 与∠ 1有什么关系？请说明。
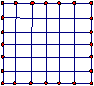
27。你玩过在方格中抠奖的游戏吗？如图，把标有奖品的6个小纸团谁机放在格子里，上面糊上一层红纸。〈1〉求抠开一个格子获奖的概率。〈2〉若有10个格子被抠开，并拿走了2个有将的纸团（抠开的格子没有被糊上），继续抠开1个格子获奖的概率是多少？〈3在〈2〉的条件下，再抠开几个没有将的纸团的格子后使得剩下没有被抠开的格子中中奖率可以为
?
28。如图，是一个较大的池塘。要想知道池塘两端A、B之间的距离。请用你所学知识设计一个解决方案，添出图形，并说明理由。
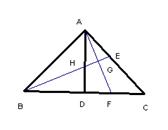
29。已知，如图，△ABC中∠BAC=90°，AB=AC，AD⊥BC于D，E为AC上一点，BE交AD于H，AF⊥BE于G，求证：DH=DF。
参考答案
一。填空。
（1）-5，1
(2) 2 (3)
54 (4) -1.100 ×10
(5)
(6)
BC=DA或∠B=∠DHUO或∠BAC=∠DCA或AB∥CD (7)y=｛
0.2 (x≦3)
0.2+0.1(x-3)[x＞3]
(8)2a<x<10a (9)x (10)12或53
二、选择题
11—15.CDCAB
16—20.DBABC
三．解答题。
2⒈(-3x+4) 22.(1) 23.(
) 24.(a-4b-c+4bc)
25.<1>乙先出发，先登山60米 〈2〉山高300米，甲登上山顶。26.∠1与∠B互为余角 27.<1> P(抠一个格子获奖)=
〈2〉P=
〈3〉10
个 28.略
29.在△ABC中,∵∠BAC=90°,AB=AC∴∠ABC=
45°又∵AD⊥BC ∴∠ADB=∠ADF=90° ∴∠BAD=45° ∴ BD=AD 又∵AF⊥BE ∴∠AGH=90° 又∵∠AHG=∠BHD ∴∠HBD=∠FAD ∴△BDH
≌△ADF ∴DH=DF。