2005学年第二学期七年级数学期末试卷
一、请在下列各空格中，仔细分析并填写（每小题3分，共27分）
1.在△ABC中, 已知∠A＝∠B, ∠B＝40°, 则∠C的度数为_________.
2.比较我们所学过的“轴对称、平移、旋转、相似”四种变换, 你认为“不改变原图形的形状、大小”的变换是__________________________.
3.假如小猫在如图所示的地板上自由地走来走去, 并随意停留在某块方砖上, 
它最终停留在黑色方砖上的概率是_________（图中每一块方砖除颜色外
完全相同）.
4.三角形的边长和周长如图所示, 若三角形的边长是整数, 则a+b=_______.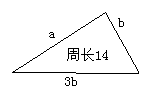
5.一块方巾铺在正方形的茶几上, 四周刚好都超出13cm, 设方巾的边长
为acm(a>13), 则这个茶几（面）的面积是_________.
6.分解因式：
_______________.
7.当
______时, 分式
的值为零.
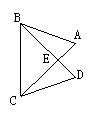
8.如图, 已知AC＝DB. 要说明△ABC≌△DCB, 只需增加一个条件是
___________________________________(写出两种不同的情况).
9.请写出一个二元一次方程组, 使它的解是
, 答: _________________.
二、四个选一个，请你对下列各题作出明智的选择（每小题3分，共27分）
10.如图, AC与BD相交于点O, 已知AB＝CD, AD＝BC, 则图中周长相等
的三角形有( )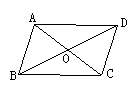 
(A)1对 (B)2对 (C)3对 (D)4对
11.从镜子里看到位于镜子对面电子钟的像如图所示, 则实际时间是( )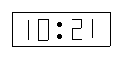 
(A)12:01 (B)10:21 (C)15:01 (D)10:51
12.袋子里装有8个红球, m个白球, 4个黑球, 它们除颜色外相同, 从中任意摸出一个球, 若
摸到白球的概率是
, 则m的值是( )
(A)4 (B)3 (C)2 (D)1
13.二元一次方程组
的解是( )
(A)
(B)
(C)
(D)
14.下列运算中, 计算结果正确的是( )
(A) a4·a＝a4 (B) a6÷a3＝a2 (C) (a3)2＝a5 (D) (ab)3＝a3b3
15.有下列多项式: ①
; ②m2＋2mn＋4n2
; ③a2＋4ab－4b2 ; ④
;
其中能用完全平方公式分解因式的个数是( )
(A) 4 (B) 3 (C) 2 (D) 1
16.计算: 
, 结果是( )
(A)
(B)
(C)
(D)
17.仓库有存煤
吨, 原计划每天烧煤
吨, 现在每天节约
吨, 则可多烧的天数为( )
(A)
(B)
(C)
(D)
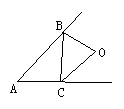
18.如图, △ABC的两个外角平分线交于点O, 设∠BOC＝
,
则∠A等于( )
(A)90°－ (B)
90°—
(C)180°－2 (D)
180°－
三、尽情发挥你的综合能力，请解答下列各题：
19.(本题共12分)看谁算得快又好:
⑴计算: 
⑵先化简, 再选择你喜欢的数代人求值: 
⑶因式分解: 4ab3－a3b ⑷解方程: 
20.(本题8分)动手画一画:
⑴已知线段AB(右图), 用直尺和圆规作线段AB的垂直平分线;
A
B
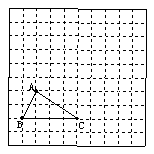
⑵把小方格中△ABC沿BA方向平移,平移的距离为线段
AB的2倍.
⑶在小方格中, 画一个钝角三角形, 使所画三角形的面积
与已知△ABC的面积相等.
21.(本题5分)在周末数学游艺会上, 李敏同学上台表演了自己“发明”的一个猜数魔术.他请每一个同学在心里随便想好一个数,不要说出来,然后按下步骤依次进行计算:
⑴这个数＋这个数；⑵所得的和×这个数；⑶所得的积－这个数；⑷所得的差÷这个数.
接着，李敏同学煞有介事地在台上转了两圈，回过头来说，我已经有了魔法.不管是谁，只要把计算结果告诉我，我就可以把你心里所想的这个数猜出来.
张小亮同学第一个站出来说：“我的结果是199，你知道我想的是什么数吗？”
李敏把手一拍，吹了一口气，就说：“你想的那个数是100，对吗？！”
张小亮点了点头，心里想，李敏的确有一套.
接着，不少同学纷纷报出了他们的计算结果，而李敏则从容不迫地一一猜出了各人所想的数.
有道是旁观者清.在座的同学，你能揭穿这个猜数魔术的奥秘吗？
22.(本题5分)用心想想: 已知方程组
, 甲同学正确解得
, 而乙同学粗心, 把
给看错了, 解得
, 求
的值.
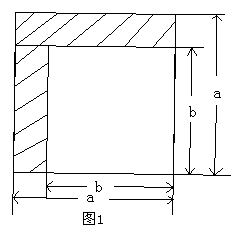
23.(本题9分)乘法公式的探究及应用:
⑴如图1所示, 可以求出阴影部分的面积是_____________(写成两数平方差的形式).
⑵若将图1中的阴影部分裁剪下来, 重新拼成一个如图2的矩形, 此矩形的面积是_________ (写成多项式乘法的形式)
 | |||
 | |||
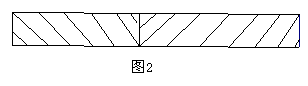(3)比较两图的阴影部分面积,可以得到乘法公式: _______________________________.
⑷应用所得的公式计算:
①10.2×9.8 ②
24.(本题7分)聘你做经理, 某商场计划拨款9万元从厂家购进50台电视机, 已知该厂家生产三种不同型号的电视机, 出厂价分别为甲种每台1500元, 乙种每台2100元, 丙种每台2500元.
⑴若商场同时购进其中两种不同型号的电视机共50台, 用去9万元, 请研究一下商场的进货方案;
⑵若商场销售一台甲种电视机可获利150元, 销售一台乙种电视机可获利200元; 销售一台丙种电视机可获利250元, 在同时购进两种不同型号电视机的方案中, 为使销售获利最多, 你选择哪种进货的方案?
七(下)期末试卷答案
1. 100° 2.
轴对称、平移、旋转 3.
4.
8
5. 
6.
7.
8.
AB＝DC或∠ACB＝∠DBC
9. 
等
10—18 DCBDD DCCC
19. ⑴
⑵
⑶
⑷
20. 略 21.
略 22.
23. ⑴
⑵
⑶
(4) ① 99.96 ② 
24. ⑴方案1：甲25台，乙25台；方案2：甲35台，丙15台
⑵选方案2