04-05学年度上学期期末模拟考试（七年级数学）
一、耐心填一填（3分×10=30分）
11．如果一次函数y=x＋b经过点A(0，3)，那么b= ．
1、49的算术平方根是_____，
的平方根是_____，－27的立方根是_____。
11、若函数
是正比例函数,则
=______。
12、拖拉机开始工作时，邮箱中有油24升，如果每小时耗油4升，那么邮箱中的剩余油量y（升）和工作时间x（时）之间的函数关系式是 。
4、若误差小于1, 则估算
的大小为 14或15
6、不等式组2≤3x－7<8的整数解为_________________________；
7、给出下列一组数：1、4、7、10、13……
其中1=3×1-2
4=3×2-2
7=3×3-2
10=3×4-2
13=3×5-2
……
据此，可猜测出第n 个数应为 经过多少时间，
15．写出两个无理数，使这两个无理数的积为有理数，那么这两个无理数可以是 和 ．
9、用火柴棒按下列方式搭正方形，照这样的方式搭下去，搭n个这样的正方形需________根火柴。
……
10、主视图、俯视图和左视图都是正方形的几何体是__________
二、精心选一选：（每题3分，共30分，将答案直接填在下表中）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1．下列各数中是无理数的是………………（ ）．
（A）2
（B）
（C）
（D）
2．9的平方根是( )．
（A）3
（B）－3 （C）±3
（D）±
8．下列一次函数中，y的值随着x值的增大而减小的是( )．
（A）y＝x （B）y＝－x （C）y＝x＋1 （D）y＝x－1
10．甲、乙两人参加植树活动，两人共植树20棵，已知甲植树数是乙的1.5倍．如果设甲植树x棵，乙植树y棵，那么可以列方程组（ ）．
（A）
（B）
（C）
（D）
14、数
，3.14，，
，1.732，
，
，
，
（相邻两个1之间的0的个数逐渐加1）中，无理数的个数为
A、1 B、2 C、3 D、4
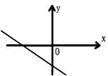21、已知一次函数
的图象如图所示,则k,b的符号是( )
A 、
B、
C、
D、
17、一个数是9，另一个数比9的相反数大2，那么这两个数的和为
（A）2 （B）-2 （C）20 （D）-20
18、下列各式从左到右正确的是
A、－(3x＋2)＝－3x＋2 B、－(－2x－7)＝－2x＋7
C、－(3x－2)＝3x＋2 D、－(－2x－7)＝2x－7
19、一个两位数，个位数字与十位数字的和是9，如果将个位数字与十位数字对调后所得新数比原数大9，则原来的两位数是（）
A．54 B．27 C．72 D．45
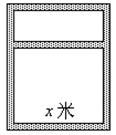20、有12米长的木料，要做成一个如图的窗框。如果假设窗框横档的长度为
米，那么窗框的面积是（ ）
（A）
（B）
（C）
（D）
三、解下列不等式（组），并把解集表示在数轴上（每小题4分，共计8分）
21. 3-2(x-4)>3x+1
22. 1- 
≥x-
 | |||
 | |||
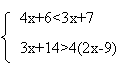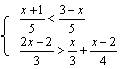23.. 24.
22．蜡烛燃烧，每小时耗去4.8厘米，已知蜡烛原来的长度为24厘米，设燃烧x小时后剩下的长度为y厘米．
（1）写出y与x之间的函数关系式；
（2）经过多长时间后，蜡烛点完？
25. k 取怎样的整数时,方程组.
的解满足 ?（5分）
四、方程解一解（6分×3＝18分）
五、开心画一画（本题6分）
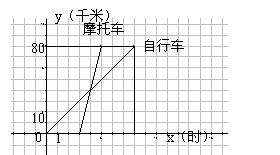28、（5分）如图是一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象（分别为正比例函数和一次函数）。两地间的距离是
80千米，请你根据图象回答或解决下面的问题。
（1） 谁出发的较早？早多长时间？
谁到达乙地较早？早到多长时间？
（2） 请你分别求出表示自行车和摩托车行驶过程的
函数解析式。
（3） 指出在什么时间段内两车均行驶在途中（不包括端点）。在这一段时间内，请你分别按下列条件列出关于时间的方程或不等式（不要化简，也不要求解）：
①自行车行驶在摩托车前面:________________________________________.
②自行车与摩托车相遇:____________________________________________.
③自行车行驶在摩托车后面:________________________________________.
（1）自行车早出发，早3小时；摩托车早到，早到3小时。
（2）自行车：y=10x
摩托车: y=40x-120
（3）在自行车出发后3-5小时之间两车均行驶在途中，即
① 
② 
③ 
（4） 请你分别求出表示自行车和摩托车行驶过程的
函数解析式。
六、理论联系实际（列方程解应用题）（6分＋6分＝12分）
23． 某电信运营商有两种手机卡，A类卡收费标准如下：无月租，每通话1分钟交费0.6元；B类卡收费标准如下：月租费50元，每通话1分钟交费0.4元。
① 分别写出A、B两类卡每月应缴费用Y（元）与通话时间x（分）之间的关系式；
② 一个用户这个月预交话费200元，按A、B两类卡收费标准分别可以通话多长时间？
③ 若每月平均通话时间为300分钟，你选择哪类卡？
④ 每月通话多长时间，A、B两类卡的费用相同？
30．某校七年级学生在作作业时，不慎将墨水瓶打翻，使得某道题只能看到如下的字样：“甲、乙两地相距160千米，摩托车的速度为45千米/时，货车的速度为35千米/时， ？”（横线部分表示被墨水覆盖的若干文字），请你将这道题补充完整，并列出方程给予解答。