第三章 《生活中的数据》复习
一、知识点：
1、 百万分之一：对较小数据的感受，用科学计数法表示绝对值较小数及单位的换算。
如：1微米= 米，1纳米= 米,4纳米= 微米= 毫米= 厘米= 米200千米的百万分之一是 米.用科学计数法表示：0.=
2、 近似数和有效数字：
一般地，通过测量的结果都是近似的。对于一个近似数从 边第 个不是 的数字起，到 的数位止，所有的数字都叫做这个数的有效数字.如：0.03296精确到万分位是 ，有 个有效数字，它们是
3、世界新生儿图：会从给出的信息图中得到有用信息；会画生动形象的统计图。
二、巩固练习：
（一）填空选择题：
1、下列数据中，是精确值的有（ ）个
（1） 在9·11恐怖事件中，估计有5000人死亡；
（2） 某细胞的直径为百万分之一米；
（3） 中国的国土面积约为960万km2
（4） 我家有3口人
（5） 一（1）班有53人
（A）1 （B）2 （C）3 （D）4
2、下列各组数据中，（ ）是精确的。
（A） 小明的身高是183.5米 （B）小明家买了100斤大米
（C）小明买笔花了4.8元 （D）小明的体重是70千克
3、 某学生测量长度用的刻度尺的最小单位是厘米
现测量一物品的结果为6.7cm ,那么 位是精确值，
位是估计值。
4、 1纳米相当于一根头发丝直径的六万分之一，那么一根头发丝的
半径为 米（用科学计数法表示）
5、一只蚂蚁的重量约为0.0002㎏，用科学计数法记为
用科学计数法表示的数3.02×10－8，其原数为
6、小东买了12.65kg苹果，精确到0.1kg，则所买苹果约为 kg
7、数0.8050精确到 位，有 个有效数字，是
8、数4.8×105精确到 位，有 个有效数字，是
9、数5.31万精确到 位，有 个有效数字，是
10、一箱雪梨的质量为20.95㎏，按下面的要求分别取值：
（1）精确到10㎏是 ㎏，有 个有效数字，它们是
（2）精确到1㎏是 ㎏，有 个有效数字，它们是
（3）精确到0.1㎏是 ㎏，有 个有效数字，它们是
11、2002年我国普通高校招生人，若精确到万位是 人
有 个有效数字，它们是 米，
12、九届人大一次会议上，李鹏同志所作的政府工作报告中指出：1997年
我国粮食总产量达到t，按要求填空：
（1）精确到百万位是 （用科学计数法表示）， 有 个有效数字，
它们是
（2）精确到亿位是 （用科学计数法表示）， 有 个有效数字，
它们是
13、数0.000125保留两个有效数字记为
14、北冰洋的面积是1475.0万平方千米，精确到（ ）位，
有（ ）个有效数字
（A）十分位，四 （B）十分位，五 （C）千位，四 （D）千位，五
15、下表是中国奥运会奖牌回眸统计表及历届奖牌总数折线图
| 届数 | 金牌 | 银牌 | 铜牌 | 总计 |
| 第23届 | 15 | 8 | 9 | |
| 第24届 | 11 | 12 | 28 | |
| 第25届 | 22 | 12 | 54 | |
| 第26届 | 16 | 16 | 50 | |
| 第27届 | 28 | 16 | 59 |
（1） 完成上表
（2） 把第23届奖牌总数在统计图上标出，并完成此折线统计图
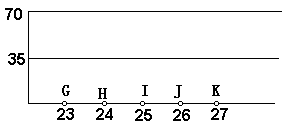
（二）解答题
1、举例说明哪些是近似数，哪些是准确数，哪些是有效数字？
2、、如图，（1）写出图中阴影部分的面积；
（2）当a=3， b=2时，计算阴影部分的面积
（
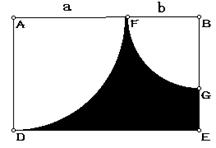=3.1415，保留3个有效数字，单位：cm）
3、随机抽取城市30天的空气质量状况统计图如下：
| 污染指数（w） | 40 | 70 | 90 | 110 | 120 | 140 |
| 天数（t） | 3 | 5 | 10 | 7 | 4 | 1 |
其中：w≤50时，空气质量为优；50＜w≤100时，空气质量为良；
100＜w≤150时，空气质量为轻微污染。
（1） 将上面的数据制成形象生动的统计图；
（2） 如果要利用面积分别表示空气质量的优、良及轻微污染，那么
这三类空气质量的面积之比为多少？
（3） 估计该城市一年（以365天计）中有多少天空气质量达到良以上；
（4） 保护环境人人有责，你能说出几种保护环境的好方法吗？
第二章 平行线与相交线 复习题
班级______________ 姓名________________ 学号_____________
一 知识点
2．1 台球桌面上的角
（1） 余角--------如果两个角的和是直角，那么称这两个角互为余角。
（2） 补角--------如果两个角的和是平角，那么称这两个角互为补角。
（3） 对顶角------两条相交直线中,有公共顶点,它们的两边互为反向延
长线的两个角叫做对顶角.(对顶角相等)
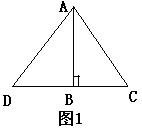
例：如右图1 互为余角的有______________________________
互为补角的有______________________________
图中有对顶角吗? 答:____________
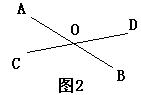
如右图2 对顶角有_______对.它们分别是____________
2 探索直线平行的条件
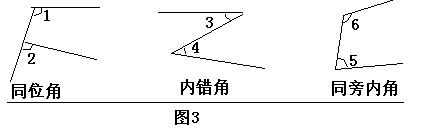
（1） 同位角，内错角，同旁内角。常见的图形如图3。
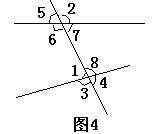
例：找出图4中的同位角，内错角，同旁内角：
同位角有_______________________________
内错角有_______________________________
同旁内角有_____________________________
（2）两直线平行的判定： 同位角____________，两直线平行。
内错角____________，两直线平行。
同旁内角__________，两直线平行。
例：如图5，由∠1=∠3得___ //____( )
由∠2=∠3得___ //____( )
由∠3+∠4=180°得___ // ____( )
由∠2+∠4=180°得___ // ____( )
2．3 平行线的特征:两直线平行，同位角___________.两直线平行，内错角____________.
两直线平行，同旁内角____________.
2．4 用尺规作线段和角
（一）用尺规作线段的步骤：
范例：已知：线段AB：
求作：线段A′B′，使得A′B′=AB。
| 作法 | 示范 | |||
| （1） 作射线A′C′；
|
A′ C′ | |||
| （2）以点A′为圆心，以AB的长为半径画弧，交射线A′C′于点B′。A′B′就是所作的线段。 |
A′ B′ C′ |
注意事项：（1）保留作图痕迹；（2）画完图后，要说明线段××就是所求。
（二） 用尺规作一个角等于已知角
二 巩固练习
一 填空：
（1）∠A的余角是20°，那么∠A等于__________度.
（2）∠A与∠B互补，如果∠A=36°，那么∠B的度数为_________.
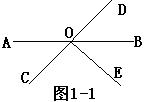
（3）如图１－１所示，∠AOC=36，∠DOE=90，则∠BOE=_______.
（4）如图１－１中，有_________对对顶角.
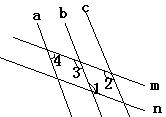
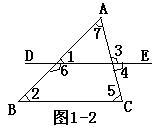
（5）如图１－２中，已知四条直线AB，BC，CD，DE。
问：①∠1=∠2是直线______和直线______被直线_____所截而成的____角. ②∠1=∠3是直线_____和直线_____被直线_____所截而成的____角.
③∠4=∠5是直线______和直线______被直线_____所截而成的____角.
④∠2=∠5是直线______和直线______被直线_____所截而成的____角.
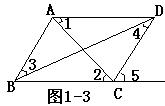
（６）如图１－３：①∵∠1=∠2，∴_____∥_____,理由是________________.
②∵AB∥DC,∴∠3=∠_______,理由是_________________.
③∵AD∥______,∴∠5=∠ADC,理由是__________________.
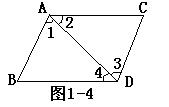
（７）如图１－４所示：
①如果∠1=∠3，可以推出______∥_______,其理由是________________②如果∠2=∠4，可以推出______∥_______,其理由是__________________
③如果∠B+∠BAD=180°,可以推出____∥____,其理由是________________
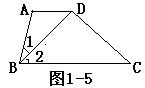
（８）如图１－５，已知AD//BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠ABC=_____，∠C=_____.
二 选择题.
(1) 若∠1与∠2的关系为内错角,∠1=40°,则∠2等于( )
A. 40° B. 140° C. 40°或140° D. 不确定
(2) 下列说法正确的是( )
A. 若两个角相等,则这两个角是对顶角.
B. 若两个角是对顶角,则这两个角是相等.
C. 若两个角不是对顶角,则这两个角不相等.
D. 所有的对顶角相等
(3) 下列说法正确的是( )
A. 有公共顶点，并且相等的两个角是对顶角
B. 两个角的两边分别在同一条直线的,这两个角互为对顶角
C. 如果两个角不相等,那么这两个角不是对顶角
D. 如果两个角相等,那么这两个角是对顶角
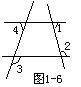
(4) 如图1-6,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
A. 50° B. 60° C.70° D.80°
(图1-10)
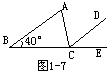
(5) 如图1-7,已知B、C、E在同一直线上，且CD//AB,若∠A=105°,∠B=40°,则∠ACE为( )
A.35° B. 40° C. 105° D. 145°
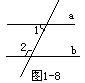
(6) 如图1-8 , a // b,,且∠2是∠1的2倍,那么∠2等于( )
A. 60° B. 90° C. 120° D. 150°
(7) 如图1-9 ,AB,CD交于点O,OE⊥AB于O,则下列说法中不正确的是( )
A.∠1与∠2是对顶角 B. ∠2与∠3是互为余角
C. ∠1和∠3是互为余角 D. ∠3和∠4是对顶角
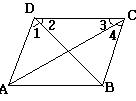
(8) 如图1-10 , 若∠1+∠2+∠3+∠4=180°,则( )
A.AD // BC B. AB // CD C. BD⊥DC D. AB⊥BC
三
解答题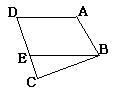
: 如右图,AB //CD ,AD // BE
,试说明∠ABE=∠D.
∵ AB∥CD (已知)
∴ ∠ABE=___________(两直线平行,内错角相等)
∵ AD∥BE (已知)
∴ ∠D=_________ ( )
∴∠ABE=∠D ( 等量代换)
第一章《整式的运算》复习
班级 姓名 学号
一、 知识点：
1、都是数与字母的乘积的代数式叫做单项式（单独的一个数或一个字母也是单项式）；几个单项式的和叫做多项式；单项式和多项式统称整式。下列代数式中，单项式共有 个，多项式共有 个。
－
, 5
, 2， ab，
, 
, a ,
, 
,
2、一个单项式中，所有字母的指数和叫做这个单项式的次数；一个多项式中，次数最高的项的次数叫做这个多项式的次数。（单独一个非零数的次数是0）
（1）单项式
的系数是 ，次数是 ；（2）π的次数是 。
（3）
是单项式
和，次数最高的项是 ，它是 次 项式，二次项是
，常数项是
3、同底数幂的乘法，底数不变，指数相加。即：
（
,
都是正整数）。填空：（1）
（2）
4、幂的乘方，底数不变，指数相乘。即：
（,都是正整数）。
填空：（1）
＝ （2）
（3）
5、积的乘方等于每一个因数乘方的积。即：
（是正整数）
填空：（1）
（2）
（3）
＝
6、同底数幂相除，底数不变，指数相减。即：
（
），
，
（
）填空：（1）
（2）
（3）
7、整式的乘法：
（1）单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。如：
。
（2）单项式与多项式相乘，
＝
（3）多项式与多项式相乘，
8、平方差公式：两数和与这两数差的积，等于它们的平方差。即：
。计算：
9、完全平方公式：
，
。
计算： （1）
（2）
10、整式的除法：单项式相除，把系数、同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的一个因式。
如：（1）
（2）
多项式除以单项式，如：
二、 巩固练习：1、选择题： （1）下列叙述中，正确的是（ ）
A、单项式
的系数是0，次数是3 B、a、π、0、22都是单项式
C、多项式
是六次三项式 D、
是二次二项式
（2）减去3
等于
的代数式是（ ）
A、
B、
C、
D、
（3）计算
的结果是（ ）
A、
B、 
C、 D、
（4）如果多项式
是一个完全平方式，则m的值是（ ）
A、±3 B、3 C、±6 D、6
（5）如果多项式
是一个完全平方式，则k的值是（ ）
A、－4 B、4 C、－16 D、16
2、计算：
（1）
（2）
（3）
（4）
（5）
（6）
3、运用整式乘法公式进行计算：
（1）899×901＋1
（2）
4、解答题：
（1） 解方程：
（2） 化简求值：
，其中
，
（3） 若
，
，求
的值
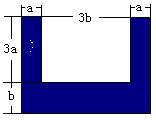
（4） 计算图中阴影部分的面积。
第四章 概率复习题
一、会判定三类事件(必然事件、不可能事件、不确定事件)及三类事件发生可能性的大小，用图来表示一件事发生可能性的大小。
1．下列事件分别是三类事件(必然事件、不可能事件、不确定事件)中的那种事件：
（1） 小明身高达到6米。______________
（2） 将一个普通玻璃杯用力摔到水泥地上，玻璃杯碎了。______________
（3） 袋中有9个球，4个黑球，5个白球，从中任意摸出一球，摸到白球。________
（4） 小明将朋友的电话号码忘了，他随意拔了几个数字，电话打通了，正好是他朋友家。______________
（5） 100个红球、1个黑球，从中任意摸一个恰好摸到红球。______________
2．必然事件发生的可能性大小是______可能事件发生的可能性大小是__________
不确定事件发生的可能性大小是__________
3．请将下列事件发生的概率标在图上：
①从三个红球中摸出一个红球
②从三个红球中摸出一个白球
③从一红一白两球中摸出一个红球
④从红、白、蓝三个球中摸出一个红
二、会判定一个游戏是否公平，并说明理由。会按题目要求设计游戏(主要是用转盘，摸球，色子)。
1．如图是一个转盘，若转到红色则小明胜，转到黑色则小东胜，这个游戏对双方是否公平？并说明理由。
 |
2．利用摸球设计一个游戏，使得摸到红球的概率为
3、请你为班会设计一个游戏，并说明在你的设计中游戏者获胜的概率是多少？
三、利用计算概率的方法计算一件事的概率。
1．袋装有红、黄、白球分别为3、4、5个，这些球除颜色外都相同，从袋中任抽一个球，则抽到黄球的概率是_________，抽到的不是黄球的概率是___________
2．将一副扑克牌除大小鬼(共52张)充分冼匀，从中任意抽一张，试求下列事件的概率。
(1)抽到红心8 (2) 抽到的牌不是红心8
四、巩固练习：1．请将下列事件发生的概率标在下图中：
 |
(1)4月25日从西边升起 ； (2) 在10瓶饮料中，有2瓶已过了保质期，从中任取一瓶，恰好是已过保质期的饮料； (3)在6张背面分别标有“1”、
“2”、“3”、“4”、“5”5个数字，且形状完全一样的卡片中任取一张恰好是“3”的卡片；
(4)在课堂数学活动，中某一小组有3名女生，2名男生，随机地指定一人为组长，恰好是女生。
2．各图：20个饮料瓶盖中,有4个红色的 ,5个
黄色的 ，其余为白色的
。现知道其中只有
一个有中奖号码，从中随意取一个
(1) 中奖号码是红色发生的概率是_________
(2) 中奖号码是黄色发生的概率是_________
(3) 中奖号码是白色发生的概率是_________
3．用1、2组成一个两位数，则组成的数是奇数的概率是_________
4．用1、2、3三个数字排成一个三位数，则排出的数是偶数的概率是________
5．任意掷一枚均匀硬币两次，两次都是同一面朝上的概率是_________
6．学校准备明天或后天举行运动会，根据天气预报可知，明天降水的概率为20%，后天降水的概率为60%，则学校在_______举行运动会为佳。
7．从生产的一批螺钉中抽取1000个进行检查，结果有4个是次品，如果从这批螺钉中任取一个，那么取到次品的概率是__________
8．P(太阳从东边升起)=_________
二、选择题：
1．下列事件中，概率P=0的事件是( )
A 某地10月16日刮西北风 B 当x是有理数时，
C 手电筒的电池没电，灯泡发亮 D 一个电影院某天的上座率超过45%
2．下列事件中，概率P=1的事件是( )
A 掷一枚硬币出现正面 B 掷一枚硬币出现反面
C 掷一枚硬币出现正面和反面 D 掷一枚硬币，或者出现正面，或者出现反面
3．如图是一个黑白小方块相间的长方形，李明用一个小球在上面随意滚动，落在黑色方块(各方块的大小相同)的概率是( )
A 
B 
C 
D 
4．从数字2,3，4中任取两个不同的数字，其积不小于8，发生的概率是( )
A B 
C 
D
三、解答题：
1．从一副52张的扑克牌中任意抽出一张，求下列事件的概率：
(1) 抽出一第红心 (2)抽出一张红色老K (3) 抽出一张梅花J
(4)抽出一张不是Q的牌
2、飞镖随机地掷在下面的靶子上。
a. 在每一个靶子中，飞镖投到区域A、B、C的概率是多少？
b. 在靶子2中，飞镖没有投在区域C中的概率是多少？
3．甲乙两种纯净水，在抽样质检中，甲的合格率为72%，乙的合格率为84%，你认为那一种纯净水对人的身体更有好处？请说明理由。
4．如图是可自动转动的转盘(转盘被分成8个在相等的扇形)。当指针指向阴影区域，则甲胜；当指针指向空白区域，则乙胜。你认为这个游戏对双方公平吗？为什么？
 |
5、个小妹妹将10盒蔬菜的标签全部撕掉了。现在每个盒子看上去都一样。但是她知道有三盒玉米，两盒菠菜，四盒豆角，一盒土豆。她随机地拿出一盒并打开它。
a. 盒子里面是玉米的概率是多少？
b. 盒子里面是豆角的概率是多少？
c. 盒子里面不是菠菜的概率是多少？
d. 盒子里面是豆角或土豆的概率是多少？
6、请设计一种游戏，使某一个事件发生的概率为0.4（提示：可用：转盘、投镖、摸球等）
第五章 三角形 复习
一、知识点：
1、三角形的三边关系：①三角形任意两边之和 第三边；②三角形任意两边之差 第三边。下列每组分别是三根小木棒的长度，用它们能摆成三角形吗？（单位：厘米。填“能”或“不能”） （1）3，4，5（ ）
（2）8，7，15（ ） （3）13，12，20（ ） （4）5，5，11（ ）
2、三角形三个内角的和等于 °。
在△ABC中，∠C=70°，∠A=50°，则∠B= 度；
3、三角形按内角的大小分为三类：①锐角三角形；②直角三角形；③钝角三角形。一个三角形两个内角的度数分别如下，这个三角形是什么三角形？
（1）30°和60° （ ）
（2）40°和70° （ ）
（3）50°和30° （ ）
4、直角三角形的两锐角 。
如上图， 在Rt△ABC中，∠A=2∠B，则∠A= 度，∠B= 度；
5、三角形的三条角平分线交于
，三条中线交于 ，三条高所在的直线交于 。三角形的角平分线、中线、高都是 （填“直线”、“射线”或“线段”）如图，在△ABC中，
（1）AD是中线，那么BD＝ ＝
，
BC＝ BD＝ DC；
（2）AE是角平分线，那么∠BAE＝ ＝ ，
∠BAC＝ ∠BAE＝ ∠EAC；
（3）AF是BC边上的高，那么∠AFB＝∠AFC＝ °，AF BC。
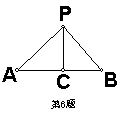6、两个能够重合的图形称为 ；
全等图形的 和 都相等；
全等三角形的对应边 ，对应角 。
如图；△ACP≌△BCP，那么
，
7、三角形全等的条件：
①三边对应相等的两个三角形全等，简写成 或
②两角和它们的夹边对应相等的两个三角形全等，简写成 或
③两角和其中一角的对边对应相等的两个三角形全等，简写成 或
④两边和它们的夹角对应相等的两个三角形全等，简写成 或
8、直角三角形全等的条件：斜边和一条直角边对应相等的两个直角三角形全等，简写成 或
二、巩固练习：（一）填空：
1、在△ABC，AB＝5，BC＝9，那么 ＜AC＜
2、一个三角形的两边长分别是3和8，而第三边长为奇数，那么第三边长是
3、已知一个等腰三角形的一边是3cm，一边是7cm，这个三角形的周长是
 |
（第4题） （第5题）
4、如上图，∠1=60°，∠D=20°，则∠A= 度
5、如上图，AD⊥BC，∠1=40°，∠2=30°，则∠B= 度，∠C= 度
6、已知△ABC中，∠A∶∠B∶∠C=1∶2∶3，则∠A＝ 度，∠B＝ 度∠C＝ 度。
7、在空白处填入“锐角”、“直角”或“钝角”：
（1） 如果三角形的三个内角都相等，那么这个三角形是 三角形；
（2）如果三角形的两个内角都小于40°，那么这个三角形是 三角形。
8、（1）已知：如图，AD∥BC，AD＝CB，你能说明△ADC≌△CBA吗？
证明： ∵AD∥BC（已知）
∴
（两直线平行，内错角相等）
在 中
∴ ≌ （ ）
（2）如图，∠B＝∠C ，AD平分∠BAC，你能证明△ABD≌△ACD？
证明：∵AD平分∠BAC（ ）
∴∠ ＝∠ （角平分线的定义）
在△ABD和△ACD中
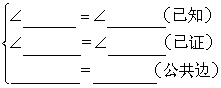
∴△ABD △ACD（ ）
（二）解答题：
1、如图，已知AB＝AC，AD是BC边上的中线，你能说明AD是角平分线吗？
证明：∵AD是BC边上的中线（已知）
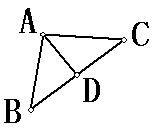∴ ＝ （中线的定义）
在 中
∴ ≌ （ ）
∴ ＝ （全等三角形的对应角相等）
∴AD是角平分线（ ）
2、如图，已知AB＝AC，AE＝AD，∠1＝∠2，你能说明△ABD≌△ACE吗？
 |
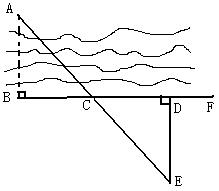
3、如图，要量河两岸相对两点A、B的距离，可以在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在一条直线上，这时测得DE的长就是AB的长，试说明理由。
 |
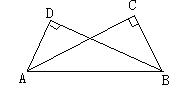
4、如图，AD＝BC，∠D＝∠C＝90°，△ABD和△BAC全等吗？
5、尺规作图：（1）已知三角形的两角及其夹边，求作这个三角形.
已知：线段∠α，∠β，线段a 。
求作：ΔABC，使得∠A=∠α，∠B=∠β，AB=a。
（2） 已知三角形的两边及其夹角，求作这个三角形.
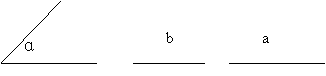已知：
求作：
7、请用全等图形设计一个你自己认为满意的图案。