太傅中学2005级初一第一学期数学竞赛题
姓名______学号＿＿＿班级______
一、 填空题：（每题2分，共38分）
1、 
单项式 
的系数 为
；次数为。
2、若
互为相反数，则mn=
3、某商人进了一批货，他以比进价高出20%的价格作为标价销售这批商品，由于市场疲软，商人只好降价格10%将商品售出，那么在这次商业活动中，此商人的利润率为 %
4、已知
，
，
，且
＞
＞
，则
＝ ；
5、若P是关于x的三次四项式，又是关于x的五次四项式，则P+Q是关于x的_______次项式。
6、绝对值小于2002的所有整数之和为 ______。
7、平面上有6条两两相交的直线，最少有______个交点，最多有________个交点。
8、已知a、b互为相反数，c、d互为倒数，x的绝对值等于1，则a+b+x2-cdx=_________。
9、观察下面一列数，按某种规律在横线上填上适当的数：
，
，
，
， ，则第
个数为
；
10、1米长的直木条，第一次截去一半，第二次截去剩下的一半，如此截下去，第六次后剩下_______，第n次后，剩下_______。
11、一次停电，小明同时点燃两支同样长度的蜡烛，已知一支蜡烛可点6小时，另一支可点4小时，恢复供电时两支蜡烛同时吹灭。小明发现其中一支蜡烛的长度只有另一支蜡烛的长度的1/4，问停电持续了_________小时。
12、一个正数x的两个平方根分别是a+1和a-3。则a=_________。x=_________。
13、一次义务劳动，团员和男同学都自愿参加，某班共有45人参加这次劳动，其中团员比男同学多5人，已知男团员有20人，则参加劳动的团员有________人，男同学有_______人。
二、 选择题：（每题3分，共36分）
1、已知a、b都是有理数，且a= —a，b≠b，则ab是（ ）
A 负数 B 正数
C 负数或零 D 非负数
2、a为有理数，下列说法中， 正确的是（ ）
A、
的值是正数 B、- 的值是负数
C、
+1的值是正数 D、-+1的值小于1
3、一个有理数的相反数与自身的绝对值的和( )
A、可能是负数 B、必为正数 C、必为非负数 D、必为0
4、已知有理数a、b、c在数轴的对应位置如下图，则a-1+a-c+a-b可化简为 。
A、b-1 B、2a-b-1
C、1+2a-b-2c D、1-2c+b
 |
5、若9人14天完成了某件工作的3/5，剩下的工作要在4天内完成。则需增加的人数是（ ）
a.10 b.11. c.12. d.13
6、设y=ax17+bx13+cx11－5，其中a、b、c为常数，已知当x=－7时，y=7则x=7时，y的值等于（ ）
A、－17 B、－7 C、14 D、21
7、设a-b=2,a-c=1/2,代数式（b-c）2+3(b-c)+9/4的值是 （ ）
A．-3/2 B. 3/2 C. 0 D. 9/4
8、若a、c、d是整数，b是正整数，且满足a+b=c,b+c=d,c+d=a那么a+b+c+d的最 大值是（ ）
A、－1 B、0 C、1 D－5
9、对所[张京明1] 有的数a, b, 把运算a※b定义为a※
b=ab-a+b. 方程5※x=17的解是( ).
(A)3
(B)2 (C)3
(D)3
10. 若[张京明2] (3a-b-4)x+(4a+b-3)y=0, 且xy≠0.
则2a-3b等于( ).
(A)-1 (B)0 (C)1 (D)2
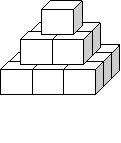
11.把14个棱长为1的正方体，在地面上堆叠成如下图所示的立体，然后将露出的表面部分涂成红色，那么红色部分的面积为 ( )
A.36 B34
C.33
D.37
12、小明小亮进行100米赛跑，第一次比赛时小明胜20米，在进行第二次比赛时，小明的起跑线比原来起跑线推后20米，如果两次他们速度不变，则第二次结果 （ ）
A、两人同时到达 B、小亮胜2米
C、小明胜2米 D、小明胜4米
三、 解答题（共26分）
1、已知：︱m︱=3/4, ︱n︱=4/3,且mn﹥0,m+n﹤0.求代数式4m2n+{-3mn2+mn-[-2mn2+(7mn-8m2n)]}的值。（8分）
2、某人乘船由A地顺流而下到B地，然后又逆流而上到C地，共用4小时，已知船在静水中的速度为7.5千米/时，水流速度为0.5千米/时，若A、C两地的距离为10千米，求A、B两地的距离。（8分）
3、如下图自然数按从小到大的顺序排列，在2处拐第一个弯，在3处拐第二弯，问拐第二十个弯的位置是哪一个数？（10）
 |
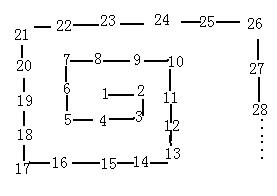四、 附加题（共20分）
1、求性质如下最小自然数：它的末位数字是6，将这个数字6移到其余数字前面，则所得的数是原数的4倍。（10）
[张京明1] (C).
[张京明2] (A)