第1章 三角形的初步知识
一、选择题(每题3分，共33分)
1、以下列各组线段为边，能组成三角形的是( )．
A．2cm、2cm、4cm B．2cm、6cm、3cm
C．8cm、6cm、3cm D．11cm、4cm、6cm
2．利用基本作图，不能作出惟一三角形的是( )。
A．已知两边及其夹角 B 已知两角及夹边
C. 已知两边及一边的对角 D. 已知三边
3．三角形的高( )．
A. 一定在三角形的内部
B. 至少有两条在三角形的内部
C. 或者都在三角形的内部，或者有两条在三角形的外部
D. 以上都不对
4、做△ABC的高AD，中线AE，角平分线AF，三者中有可能画在△ABC外的是( )
A、中线AE B、高AD C、角平分线AF D、都有可能
5、如图，△ABC的角平分线AD、中线BE交于点O，则结论：①AO是△ABE的角平分线；②BO是△ABD的中线。其中( )．
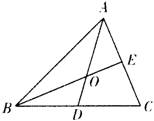
A. ①、②都正确 B．①、②都不正确
C. ①正确，②不正确 D．①不正确，②正确
6．已知△ABC的外角∠CBE和∠BCF的角平分线BP、CP交于点P，则∠BPC是( )．
A．钝角 B．锐角 C．直角 D．无法确定
7.有下列关于两个三角形全等的说法: ㈠三个角对应相等的两个三角形全等;㈡三条边对应相等的两个三角形全等;㈢两角与一边对应相等的两个三角形全等;㈣两边和一角对应相等的两个三角形全等.其中正确的个数是：（ ）
(A)1 (B)2 (C)3 (D)4
8. ΔABC中的两条角平分线BD,CE相交于点P,若
,则∠BPC的度数是: ( )
(A)
(B)
(C)
(C)
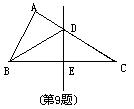
9.如图,在ΔABC中,BC边上的垂直平分线交AC于点D,
已知AB=3,AC=7,BC=8,则ΔABD的周长为:
(A)10 (B)11 (C)15 (D)12
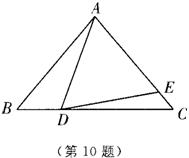
10． 如图，在△ABC中，AB＝AC，AD＝DE，∠BAD＝20°，∠EDC＝10°，则∠DAE的度数为( )．
A．30° B．40° C．60° D．80°
11．下列四组中一定是全等三角形的是( )．
A．三内角分别相等的两个三角形 B．斜边相等的两个直角三角形
C．周长相等的两个等边三角形 D．面积相等的两个等腰三角形
二、填空题(每题3分．共21分)
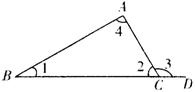
11．如图，∠1∶∠2∶∠3＝1∶2∶3，则∠4＝________。
12．已知BD、CE是△ABC的高，直线BD、CE相交所成的角中有一个角为70°，则∠BAC＝________°。
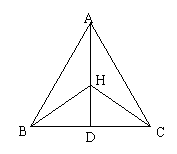
13、如图，△ABC中，AD垂直平分BC,H是AD上一点，连接BH,CH.写出AD平分∠BAC的理由＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
14．在△ABC中，AB＝3，BC＝7，则AC的取值范围是________。
15．若三角形的：三个外角的度数之比为3∶2∶4，则三个内角的度数之比为 。
16．直角三角形两锐角的平分线所成角的度数是________度。
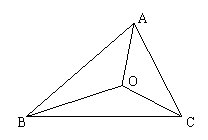
17.如图，D是△ABC内任意一点，连接DA、DB、DC.
试说明：DA+DB+DC>(AB+BC+CA)
理由＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
三、解答题(第18、19、20题每题6分，第21、22每题8分，第23、24题每题6分，共46分)
18、已知△ABC的周长是12cm，a，b，c是△ABC的三边，且c＋d＝2b，c－a＝2cm，求a，b，c的长。
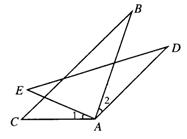19．如图，AC=AE，AB=AD，∠1=∠2。请说明下列结论成立的理由：
(1) △ABC≌△ADE； (2)BC=DE。
20.如图,PB平分∠ABC,AC和BP垂直,PD⊥BC,PE⊥AB,D,E分别为垂足.
(1) 说明ΔABP≌ΔCBP的理由;
(2) 说明AE=CD的理由.
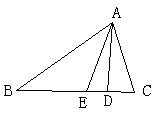
21.如图：已知△ABC中，AD⊥BC于D，AE为∠A的平分线，且∠B=35°，∠C=65°求∠DAE的度数。
22．如图．在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件．请你在其中选三个作为已知条件，余下的一个作为结论，写出—个正确的结沦，并说明理由。
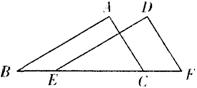
①AB＝DE；②AC＝DF；③∠ABC＝∠DEF；④BE＝CF．
已知：
结沦：
理由：
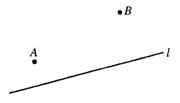
23．如图，直线l表示一条公路，点A,点B表示两个村庄。现要在公路上造一个车站，并使车站到两个村庄A，B的距离相等，问车站建在何处？请在图上标明地点，并说明理由。(要求尺规作图，不写作法)
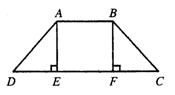
24．(8分)如图，四边形ABCD是一防洪堤坝的横截面，AE⊥CD，BF⊥CD，且AE=BF，∠D=∠C，问：AD与BC是否相等？说明你的理由。
解：在△ADE和△BCF中，
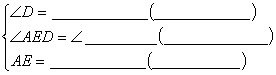
∴△ADE≌△BCF(___________________)
∴AD=BC(______________________________)