2006年七年级下学期数学试题
期中考试
(满分120分，时间120分钟)
一、选择题（每小题3分，共30分）
1．数学课上老师给出下面的数据，（ ）是精确的
A、2002年美国在阿富汗的战争每月耗费10亿美元
B、地球上煤储量为5万亿吨以上
C、人的大脑有1×1010个细胞
D、七年级某班有51个人
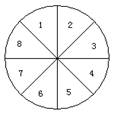
2．如图，圆盘被等分成8个扇形，转盘上的指针可以自由地转动，如果指针不会停留在分界线上，那么指针停留在偶数区域的概率是（ ）
A、
B、
C、
D、1
3．代数式
，
，
，
中，单项式的个数是（ ）
A、4个 B、3个 C、2个 D、1个
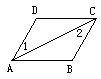4．如图，∠1＝∠2，由此可得哪两条直线平行（ ）
A、AB∥CD B、AD∥BC
C、A和B都对 D、无法判断
5．下面四个图形中∠1与∠2是对顶角的图形有（ ）个
A、0 B、1 C、2 D、3
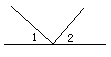
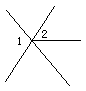
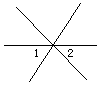
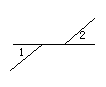
6．下列等式成立的是（ ）
A、
B、
C、
D、
7．长荆铁路使武汉至宜昌的铁路全程只有260千米，它的百万分之一，相当于（ ）
A、你自己的身高 B、一张课桌的长度
C、数学期中考试卷的宽度 D、黑板长度
8．近似数
用科学记数法表示，应该是（ ）
A、
B、
C、
D、
9．如果一个角的两边平行于另一个角的两边，那么这两个角（ ）
A、相等 B、互补 C、互余 D、相等或互补
10．如图，在方格纸中有四个图形<1>、<2>、<3>、<4>，其中面积相等的图形是（ ）
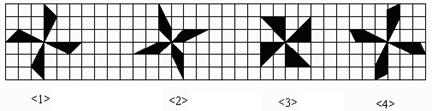
A、 <2>和<3> B、 <1>和<2> C、 <2>和<4> D、 <1>和<4>
二、填空题（每小题2分，共10分）
11．单项式
的系数是_________，次数是________
12．若∠1和∠2互为余角，且∠1＝30°，则∠2＝________°
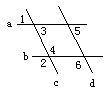13.计算
＝_________
14．在制作“人口图”时，小明用长方形近似地表示山西省，若1平方毫米表示10万人，而山西省人口总数约为3297万人，则这个长方形面积约为____________平方毫米（结果保留2个有效数字）
15．如图，如果希望
∥
，那么需要图中哪些角相等___________________
三、计算题（每小题5分，共20分）
16．
17.
18．
19.
四、解答题(每小题6分，共42分)
20．请你利用扑克牌、转盘、骰子、硬币等设计一个游戏，并且让你自己的获胜的概率是75%，加以必要的说明。
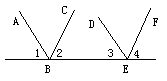
21．完成下列推理说明：
如图，已知AB∥DE，且有∠1＝∠2，∠3＝∠4，
∵AB∥DE（已知）
∴∠1＝∠3（__________________________）
∵∠1＝∠2，∠3＝∠4(已知)
∴∠2＝∠4（等量代换）
∴BC∥EF（___________________________）
22．作图：已知∠1和∠2如下图所示，用尺规作图画出∠AOB＝∠1+∠2，保留作图痕迹
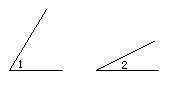
23．小康村正在进行绿地改造，原有一正方形绿地长为
米，现将它每边增加3米，面积则增加了多少平方米？
24．下面是《NBA2003-04常规赛季火箭赛程及姚明技术统计表》的一部分数据：
| 日期 | 对阵（后者主场） | 得分 |
| 4月5日 | 国王99-94火箭 | 21 |
| 4月7日 | 火箭90-97勇士 | 15 |
| 4月8日 | 火箭102-97快船 | 12 |
| 4月10日 | 掘金103-106火箭 | 12 |
| 4月11日 | 火箭69-82爵士 | 15 |
请依据上表中数据回答以下问题：
（1） 姚明第五场球得分多少？____________________
（2） 这五场球中姚明得分最高的是多少？最低得分是多少？_______________________
（3） 请设计适当的统计图来表示姚明在这五场球赛中的表现：
25．在第23小题中，有居民提议在绿地中修建一个半径为r的圆形喷水池，并在其它部分铺上新的草皮，要求水池离绿地边有一定的间隔。（1）请画出你的设计方案；（2）新植的草皮面积为多少？
26．化简求值：
，其中
五、发展思维题（每小题6分，共18分）
27．小明和小强平时是爱思考的学生，他们在学习《整式的运算》这一章时，发现有些整式乘法结果很有特点，例如：
，
，
小明说：“这些整式乘法左边都是一个二项式跟一个三项式相乘，右边是一个二项式”，
小强说：“是啊！而且右边都可以看成是某两项的立方的和（或差）”
小明说：“还有，我发现左边那个二项式和最后的结果有点像”
小强说：“对啊，我也发现左边那个三项式好像是个完全平方式，不对，又好像不是，中间不是两项积的2倍”
小明说：“二项式中间的符号、三项式中间项的符号和右边结果中间的符号也有点联系”
…… ……
亲爱的同学们，你能参与到他们的讨论中并找到相应的规律吗？
（1）能否用字母表示你所发现的规律？
（2）你能利用上面的规律来计算
吗？
28．Windows2000下有一个有趣的游戏“扫雷”，下图是扫雷游戏的一部分：
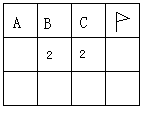说明：图中数字2表示在以该数字为中心的8个方格中有2个地雷，小旗表示该方格已被探明有地雷，现在还剩下A、B、C三个方格未被探明，其它地方为安全区（包括有数字的方格）。
（1） 现在还剩下几个地雷？
（2）A、B、C三个方格中有地雷的概率分别是多大？
29．如图，已知AB∥CD，∠A＝∠C，若∠ADB＝65°，求∠DBC的度数
