初一数学第一次阶段性练习
班级________学号_______姓名_____________
一、选择题:(每题3分,共30分)
1、下列长度的各组线段能构成三角形的是 ( )
A、4㎝,4㎝,9㎝ B、3㎝,8㎝,5㎝ C、4㎝,5㎝,6㎝ D、4㎝,5㎝,10㎝
 2、下图是各种汽车的标志,其中是轴对称图形的个数是( )
2、下图是各种汽车的标志,其中是轴对称图形的个数是( )
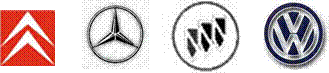
A、 4个 B、 3个 C、 2个 D、 1个
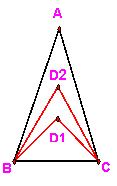
3、如图,在ΔABC中,∠A=52O,∠ABC 与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依次类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是:( )
A、56O B、60O C、68O D、94O
4、下列事件中是随机事件的是( )
A、火车开到月球上 B、在图形的旋转变换中,面积不会改变
C、抛出的石子会下落 D、掷一枚硬币,停止后正面朝上
5、某商店举办有奖销售活动,办法如下:凡购货满100元者得奖券一张,多购多得。每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个。那么买100元商品的中奖概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、下列各方程组中,属于二元一次方程组的是( )
A、 ![]() B、
B、 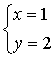 C、
C、 ![]() D、
D、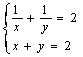
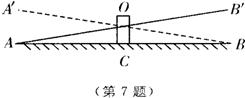
7、如图是跷跷板的示意图,支柱OC与地面垂直,点O是横板AB'的中点,AB'可以绕着点O上下转动,当A端落地时,∠OAC=10°,则横板上下可转动的最大角度(即∠A'OA)是( )
A、 10° B、20° C、30° D、 40°
8、如图8,D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,则( )
A、当∠![]() 为定值时,∠CDE为定值 B、当∠B为定值时,∠CDE为定值
为定值时,∠CDE为定值 B、当∠B为定值时,∠CDE为定值
 C、当∠
C、当∠![]() 为定值时,∠CDE为定值 D、当∠
为定值时,∠CDE为定值 D、当∠![]() 为定值时,∠CDE为定值
为定值时,∠CDE为定值
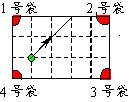 9、如图,是一个经过改造的台球桌面示意图,图中四个角上的
9、如图,是一个经过改造的台球桌面示意图,图中四个角上的
阴影部分分别表示四个入球孔。如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
![]() 、四号袋
、四号袋 ![]() 、三号袋
、三号袋 ![]() 、二号袋
、二号袋 ![]() 、一号袋
、一号袋
 10、如图,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,
10、如图,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,
AD=5,则图中阴影部分的面积为( )
A、6 B、7.5 C、15 D、30
二、填空题:(每题2分,共20分)
 1、如果一个正多边形绕它的中心旋转至少
1、如果一个正多边形绕它的中心旋转至少![]() 才能和原来的图形重合,则这个多边形是
。
才能和原来的图形重合,则这个多边形是
。
2、方程![]() 的所有正整数的解
的所有正整数的解
是 。
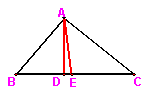
3、如图,AD、AE分别是△ABC的高和角平分线,∠B=60°,
∠C=40°,则∠CAD=________,∠DAE=________。
 4、如果
4、如果![]() 与
与![]() 是同类项,则
是同类项,则![]() ,
,![]() 。
。
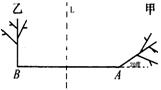
5、如右图,请说出甲树是怎样由乙树变
换得到的:
。
6、已知二元一次方程![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 为
。
为
。
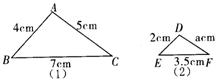 7、如图,图(2)是由图(1)经过相似变
7、如图,图(2)是由图(1)经过相似变
换后所得的像,则![]() =
。
=
。
8、我们把形如![]() 的四位数称为“对称数”,如1991、2002等。在1000~10000之间有 个“对称数”。
的四位数称为“对称数”,如1991、2002等。在1000~10000之间有 个“对称数”。
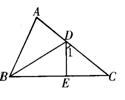 9、如图,在⊿ABC中,已知AD=ED,AB=EB,
9、如图,在⊿ABC中,已知AD=ED,AB=EB,
∠A=80O,则∠1+∠C= 度。
10、两个人在一起做“锤子、剪子、布”的游戏,在一个回合中两人都出“剪子”的概率是___________。
三、解答题(共50分)
1、解方程组(共8分):
(1) ![]() (2)
(2)
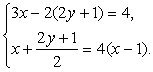
 2、(5分)如图,在
2、(5分)如图,在![]() 中,DE是AC的垂直平分线,AE=5㎝,
中,DE是AC的垂直平分线,AE=5㎝,![]() 周长为13㎝,求
周长为13㎝,求![]() 的周长。
的周长。
 3、(4分)有人说,自己的步子大,一步能走三米多,你相信吗?用你学过的数学知识说明理由。
3、(4分)有人说,自己的步子大,一步能走三米多,你相信吗?用你学过的数学知识说明理由。
4、(4分)如图,画出将△ABC向右平移2个单位,再向上平移2个单位后的图形。
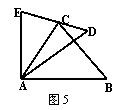 5、(6分)已知:如图5,AE=AC, AD=AB,∠EAC=∠DAB,
5、(6分)已知:如图5,AE=AC, AD=AB,∠EAC=∠DAB,
求证:△EAD≌△CAB.
6、(6分)甲、乙两人各自投掷一个普通的正方体骰子,如果两者之积为奇数,那么甲得1分;如果两者之积为偶数,那么乙得1分,连续投掷20次,谁得分高,谁就获胜.
(1)请你想一想,谁获胜的可能性(机会)大?简要说明理由.
(2)你认为这个游戏公平吗?如果不公平,请为他们设计一个公平的游戏.
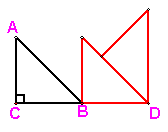
7、(5分) 如图,△ABC中,∠ACB=90o,直角边AC=BC=5厘米,把△ABC沿CB方向平移5厘米,再绕点D按顺时针方向旋转45o,则△ABC在变换过程中所经过的面积是多少?(![]() )
)
8、(6分)“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化为简单的问题,把抽象的问题转化为具体的问题。
(1)
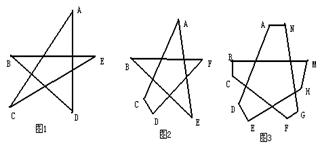 根据已经学过的知识我们知道星形(图1)中∠A+∠B+∠C+∠D+∠E=
根据已经学过的知识我们知道星形(图1)中∠A+∠B+∠C+∠D+∠E=![]() ,若对图1中星形截去一个角,如图2,请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数。(需要写出解题过程)
,若对图1中星形截去一个角,如图2,请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数。(需要写出解题过程)
(2)若再对图2中的角进一步截去,你能由题1中所得的方法或规律,猜想出图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?(只要写出结论,不需要写出解题过程。)
9、 (6分)已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
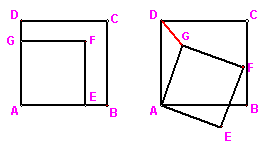 (1)如图1, 连结DF、BF, DF与BF相等吗?(不需说明理由),若将正方形AEFG绕点A按顺时针方向旋转,判断“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由;若不正确,请举出反例;
(1)如图1, 连结DF、BF, DF与BF相等吗?(不需说明理由),若将正方形AEFG绕点A按顺时针方向旋转,判断“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由;若不正确,请举出反例;
(2)若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.