第二章《一元二次方程》测试题
一、填空题(每小题3分，共30分)
1．当a _________时，方程 (a2－1)x2 + 3ax + 1＝0 是一元二次方程．
2．将方程(2x)2＝(x + 1)2化为一元二次方程的一般形式为_______.
3．已知关于x的方程x2 －ax－3a＝0的一个根是－2，则它的另一个根是_________
4．方程(x－ 1)2－2(x－1)＝0的根为_______；方程(x－1)2 － 9 = 0 的根为_______
5．当x＝_______ 时，代数式3－ x 和－x2 + 3x 的值互为相反数
6．一元二次方程x2 + x －1＝0 的根是____________.
7．两个连续自然数的平方和比它们的和的平方小112，那么这两个自然数是________________
8．把一根长度为14cm的铁丝折成一个矩形，这个矩形的面积为12cm2，则这个矩形的对角线长是________________cm.
9．直角三角形斜边同它的一条直角边的比是13：12，而另一条直角边的长是15cm，则这个三角形的周长是_______.
10．某农机厂10个月完成了全年的生产任务，已知10月份生产拖拉机1000台，为了加速农业机械化，该厂计划在年底前再生产2310台，求11月、12月平均每月的增长率，这个问题中，若设平均增长率为x，则所得的方程是________________.
二、选择题（每小题3分, 共18分）
11. 若 (b－1)2 + a2 = 0, 则下列方程中是一元二次方程的是 ( )
A. ax2 + 5x －b = 0 B. (b－1)x2 + (a + 3)x －5 =0
C. (a－1) x2 + (b－1)x－7 = 0 D. (b－1) x2 + ax －1 = 0
12．关于x的方程m2 x3 + mx2 = m2x3 + nx2 + px + q( 其中 m ≠ 0)，经过化简整理, 化成ax2 + bx + c＝0 的形式，其中a，b，c 分别是 ( )
A. a = m－n , b = p, c = q B. a＝m－n，b＝－p, c＝q
C．a ＝m－ n , b ＝ －p, c= －q D. a = m－n b = p, c ＝ －q
13．用配方法解关于x的方程x2 + px + q = 0时，此方程可变形为 ( )
A.. 
B.
C. 
D. 
14．方程x (x + 3)(x－2)＝0的根是 ( )
A. 2，－3 B. －2，3 C. 0，2，－3 D. 0,－2，3
15．生物兴趣小组的学生，将自己收集的标本向本组其他成员各赠送一件，全组共互赠了182件，如果全组有x名同学，则根据题意列出的方程是 ( )
A. x (x + 1) = 182 B. x (x －1) = 182
C. 2x ( x + 1) = 182 D. x (x－1) = 182×2
16．哈尔滨市政府为了申办2010年冬奥会，决定改善城市容貌，绿化环境，计划过两年时间，绿地面积增加44％，这两年平均每年绿地面积的增长率是 ( )
A. 19％ B. 20％ C. 21％ D. 22％
三、解答题 (共52分)
17．用适当的方法解下列方程(每小题4分，共16分)
(1)
3x2 －2x ＝ 0； (2)
(3)
x2 + x －3 ＝ 0； (4)
18．(6分) 已知三角形两边分别为3和8，第三边是方程x2 －17ｘ＋70 ＝0的根，求此三角形的周长．
19．(7分) 若规定两数a, b 通过“※”运算, 得到4ab, 即 a※b = 4ab , 例如
2※6 = 4×2×6 = 48.
(1) 求 3※5的值.
(2) 求x ※x + 2 ※x －2※4 = 0 中x 的值.
20．(7分)某商场在“五一节”的假日里实行让利销售，全部商品一律按九销售，这样每天所获得的利润恰是销售收入的20%，如果第一天的销售收入4万元，且每天的销售收入都有增长，第三天的利润是1.25万元，
（1） 求第三天的销售收入是多少万元？
（2）求第二天和第三天销售收入平均每天的增长率是多少？
21. (8分)用一块长方形的铁片, 把它的四角各剪去一个边长为4cm的小方块, 然后把四边折起来, 做成一个没有盖的盒子, 已知铁片的长是宽的2 倍, 做成盒子的容积是 1536 cm3, 求这块铁片的长和宽.
22. (8分) 阅读下列材料, 解答问题:
阅读材料:
为解方程 (x2 －1 )2 － 5(x2 －1 ) + 4 = 0, 我们可以将x2 －1视为一个整体, 然后设 x2 －1 = y , 则 (x2 －1 )2 = y2, 原方程化为 y2 － 5y + 4 = 0 .
解得 y1 = 1, y2 = 4.
当 y = 1 时, x2 －1 = 1 , ∴ x 2 = 2, ∴x = 
当 y = 4 时, x2 －1 = 4 , ∴ x 2 = 5, ∴x = 
.
∴原方程的解为 
解答问题 ：
(1)填空：在由原方程得到的过程中, 利用______________达到了降次的目的, 体现了_____________的数学思想.
(2)解方程x 4 －x 2 －6 = 0.
附加题：
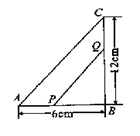23．如图, 在△ABC中, ∠B = 90°, 点P从点 A 开始沿AB边向点B以 1cm / s 的速度移动, 点Q 从点B开始沿 BC 边向C点以 2 cm / s 的速度移动, 如果点P、Q分别从A、B同时出发, 几秒钟后, △PBQ 的面积等于8 cm2
?