七年级《二元一次方程组》测试卷
班级 队别 姓名 得分
一、填空题（每空2分，共28分）
1、把方程2x－y－5＝0化成含y的代数式表示x的形式：x＝ ．
2、在方程3x－ay＝8中，如果
是它的一个解，那么a的值为
。
3、已知二元一次方程2x－y＝1，若x＝2，则y＝ ，若y＝0，则x＝ ．
4、方程x＋y＝2的正整数解是__________
5、某人买了60分的邮票和80分的邮票共20张，用去了13元2角，则60分的邮票买了 枚，80分的邮票买了 枚。
6、若3xn－1y2－m和－2x4＋myn＋1是同类项，则m=_______,n=________.
7、若∣x－2y＋1∣＋∣x＋y－5∣＝0，则x＝ ，y＝ 。
8、大数和小数的差为12，这两个数的和为60，则大数是 ，小数是 。
9、某种植大户计划安排10个劳动力来耕作30亩土地，这些土地可以种蔬菜也可以种水稻，种这些作物所需劳动力及预计产值如下表：
| 每亩所需劳动力（个） | 每亩预计产值（元） | |
| 蔬 菜 |
| 3000 |
| 水 稻 |
| 700 |
为了使所有土地种上作物，全部劳动力都有工作，应安排种蔬菜的劳动力为 人，这时预计产值为 元。
二、选择题（本题共有8个小题，每小题3分，共24分）
10、一个二元一次方程的解集，是指这个方程的（ ）
A 一个解 B 两个解 C 三个解 D 所有解组成的集合
11、在方程2(x+y)－3(y－x)=3中，用含x的一次式表示y，则（ ）
A y=5x－3 B y=－x－3 C y=
D y=－5x－3
12、下列各方程组中，属于二元一次方程组的是（ ）
A 
B 
C 
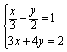D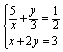 
13、方程组
的解是（
）
A 
B 
C 
D 
14、已知
的解是
，则（
）
A 
B 
C 
D 
15、一年级学生在会议室开会，每排座位坐12人，则有11人无处坐；每排座位坐14人，则余1人独坐一排，则这间会议室共有座位排数是（ ）
A 14 B 13 C 12 D 155
16、用加减法解方程组
时，有下列四种变形，其中正确的是（ ）
A 
B 
C 
D 
17、从1999年11月1日起，全国储蓄存款征收利息税，税率为利息的20%，即储蓄利息的20%由各银行储蓄点代扣代收。某人在1999年12月存入人民币若干元，年利率为2.25%，一年到期后将缴纳利息税72元，则他存入的人民币为（ ）
A 1600元 B 16000元 C 360元 D 3600元
三、解答题
解下列方程组（每题6分，共24分）
（18）
（19）
（20）
（21）
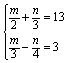
列方程组解下列应用题（共44分）
22、一个学生有中国邮票和外国邮票共325张，中国邮票的张数比外国邮票的张数的2倍少2张，这个学生有中国邮票和外国邮票各多少张？（8分）
23、某人用24000元买进甲、乙两种股票，在甲股票升值15％，乙股票下跌10％时卖出，共获利1350元，试问某人买的甲、乙两股票各是多少元？（8分）
24、某城市出租车收费标准为：起步价（3千米）6元；3千米后每千米1.20元。翁老师一次乘了8千米，花去12元；第二次乘了11千米，花去15.60元。
请你编制适当的问题，列出相应的二元一次方程组，写出求解过程。（9分）
25、甲、乙两班学生到集市上购买苹果，苹果的价格如下：
| 购买苹果数 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
甲班分两次共购买苹果70千克（第二次多于第一次），共付出189元；而乙班则一次购买苹果70千克，
（1）乙班比甲班少付出多少元？
（2）甲班第一次、第二次分别购买多少千克？（9分）
26、阅读小故事,列出满足题意的二元一次方程组
(杨损问题)唐朝时,有一位懂数学的尚书叫杨损,他曾主持一场考试,其中有一道题是:"有一天,几个盗贼正在商议怎样分配偷来的布匹,贼首说,每人分六匹布,还剩下五匹布;每人分七匹布还少了八匹布.这些话被躲在暗处的衙役听到了,他飞快地跑回官府,报告了知府,但知府不知道有多少盗贼,不知派多少人去抓捕他们.请问:有盗贼几人,布匹多少?
列出二元一次方程组，并根据问题的实际意义找出问题的解。
加工某种产品需经两道工序，第一道工序每人每天可完成900件，第二道工序每人每天可完成1200件，现有7位工人参加这两道工序，应怎样安排人力，才能使每天第一、第二道工序所完成的件数相等。